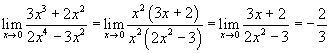|
|
|
\require{AMSmath}



Re: Limieten van funkties
Hallo Tom,
Ik geloof dat je me toch wat verder zal moeten helpen.
Moet ik de afgeleiden nemen van een quotiŽnt en dan x op nul invullen.IK zie het niet klaar voor mij.
Nog wat hulp please?
Groeten,
Rik
lemmen
Ouder - dinsdag 18 april 2006
Antwoord
Beste Rik,
Er komen helemaal geen afgeleiden aan te pas. Dat kan wel, bij onbepaaldheden, door L'Hopital toe te passen. Soms lukt het daar niet mee, of moet je het zodanig vaak toepassen dat het hopelijk ook eenvoudiger kan.
Wat we hier doen is sin(x), tan(x) en cos(x) vervangen door respectievelijk x, weer x en 1. Deze benadering kunnen we maken omdat we de limiet voor x gaande naar 0 nemen, het zijn de eerste-orde termen in hun Taylor reeksen.
Als voorbeeld de eerste opgave, die gaat dan over in:
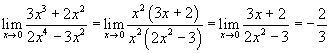
De tweede limiet zal niet bestaan, de functie divergeert in x = 0.
mvg,
Tom

|
Vragen naar aanleiding van dit antwoord? Klik rechts..!
dinsdag 18 april 2006
|

|



home |
vandaag |
bijzonder |
gastenboek |
statistieken |
wie is wie? |
verhalen |
colofon
©2001-2024 WisFaq - versie 3
|








 Dit is een reactie op vraag 44969
Dit is een reactie op vraag 44969