|
|
|
\require{AMSmath}
Re: Vierkanten op een stippenrooster
Bij 5 bij 5 is hoeveel vierkant?
Berliu
Leerling bovenbouw havo-vwo - woensdag 5 juni 2019
Antwoord
Als je het antwoord bestudeert dan kan je de volgende tabel maken voor een stippenpatroon van 8 bij 8:
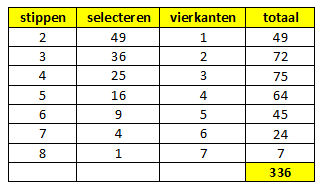
Je komt dan uit op 336 verschillende vierkantjes.
Meer in het algemeen zou je dat ook voor 2x2, 3x3, 4x4, ... kunnen doen. Dat ziet er dan (ongeveer) zo uit:
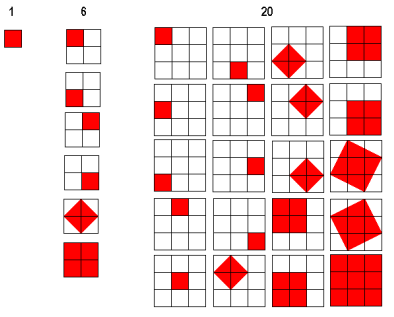
De vraag is nu hoeveel vierkantjes kan je maken voor een stippenpatroon van 5 bij 5. Je kunt dan onderstaande tabel invullen op dezelfde manier als bij de tabel hierboven en dan weet je het...
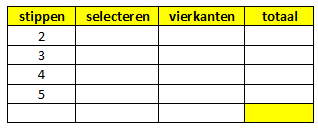
Als het goed is kom je dan uit op 50 vierkantjes.
Hieronder zie je nog de tabel voor n=2...10
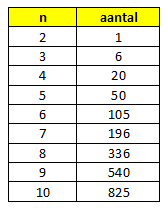
De algemene formule daarvoor is:
$
\eqalign{\sum\limits_{k = 2}^n {(n - k + 1)^2 \cdot (k - 1)} = \frac{{n^2 (n^2 - 1)}}
{{12}}}
$
Zie 4-dimensional pyramidal numbers
|
Vragen naar aanleiding van dit antwoord? Klik rechts..!
woensdag 5 juni 2019
|
|
home |
vandaag |
bijzonder |
gastenboek |
statistieken |
wie is wie? |
verhalen |
colofon
©2001-2024 WisFaq - versie 3
|
Dit is een reactie op vraag 1602