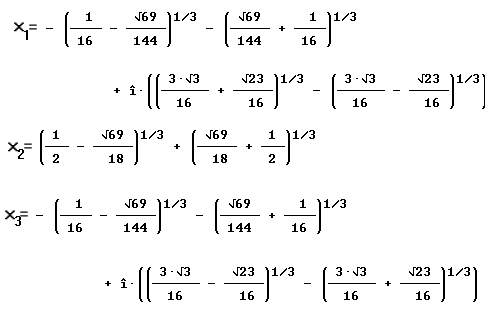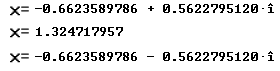WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Het oplossen van de vergelijking voor het plastische getal

Beste

Ik heb al heel wat informatie gevonden over het plastische getal. Ik weet al dat het de reële oplossing is van de vergelijking $x^3=x-1$ en ik weet hoe dat je het berekent.

Ik weet ook dat er twee andere complexe oplossingen zijn. Maar hoe kan je die berekenen? Met mijn kennis van de complexe getallen kom ik er niet...

Alvast bedankt
Ala
Leerling bovenbouw havo-vwo - vrijdag 27 maart 2020

Antwoord

Je vergelijking klopt niet. Dat moet $x^3=x+1$ zijn. Voor het oplossen van vergelijking als $-x^3+ax^2+bx+c=0$ kan je het volgende algoritme gebruiken.

$
\eqalign{
& Gegeven: - x^3 + ax^2 + bx + c = 0 \cr
& p: = \frac{2}
{3}\sqrt {a^2 + 3b} \cr
& q: = - \frac{{2a^3 + 9ab + 27c}}
{{2\sqrt {(a^2 + 3b)^3 } }} \cr
& x_1 : = p \cdot \cos \left( {\frac{1}
{3}\arcsin \left( q \right) - \frac{1}
{2}\pi } \right) + \frac{1}
{3}a \cr
& x_2 : = p \cdot \cos \left( {\frac{1}
{3}\arcsin \left( q \right) + \frac{1}
{6}\pi } \right) + \frac{1}
{3}a \cr
& x_3 : = p \cdot \cos \left( {\frac{1}
{3}\arcsin \left( q \right) + \frac{5}
{6}\pi } \right) + \frac{1}
{3}a \cr}
$

Het invullen van de juiste waarden geeft:

$
\eqalign{
& a = 0 \cr
& b = 1 \cr
& c = 1 \cr
& p = 1\frac{1}
{2}\sqrt 3 \cr
& q = - 1\frac{1}
{2}\sqrt 3 \cr}
$

Je krijgt dan 3 oplossingen:

$
\eqalign{
& x_1 : = 1\frac{1}
{2}\sqrt 3 \cdot \cos \left( {\frac{1}
{3}\arcsin \left( { - 1\frac{1}
{2}\sqrt 3 } \right) - \frac{1}
{2}\pi } \right) \cr
& x_2 : = 1\frac{1}
{2}\sqrt 3 \cdot \cos \left( {\frac{1}
{3}\arcsin \left( { - 1\frac{1}
{2}\sqrt 3 } \right) + \frac{1}
{6}\pi } \right) \cr
& x_3 : = 1\frac{1}
{2}\sqrt 3 \cdot \cos \left( {\frac{1}
{3}\arcsin \left( { - 1\frac{1}
{2}\sqrt 3 } \right) + \frac{5}
{6}\pi } \right) \cr}
$

De oplossingen kan je uitschrijven als:

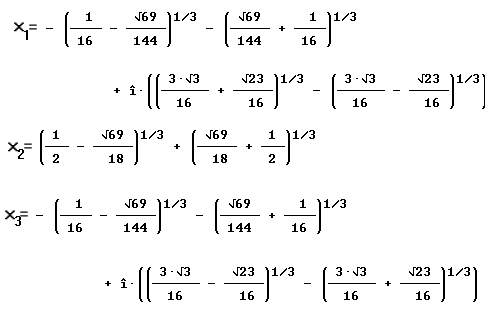
Eén reële en twee complexe oplossingen. Als je de oplossingen benadert dan zie je het plastische getal verschijnen bij de tweede oplossing.

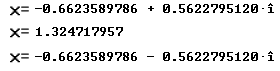
Je kunt ook 's kijken op x³=x+1 voor een andere schrijfwijze die (hopen we dan maar) op hetzelde neerkomt.

Volgens mij zijn we er dan wel uit...

Vragen naar aanleiding van dit antwoord? Klik rechts..!
zaterdag 28 maart 2020