|
|
|
\require{AMSmath}



De oppervlakte en inhoud van een tetraŽder
Ik had nog een aantal vragen over het berekenen van de oppervlakte van bijvoorbeeld de tetraŽder. Hoe berekenen ze de hoogtelijn dmv pythagoras? Er moet 1/2a√3 uitkomen....
Als je het grondvlak hebt berekend kan je de inhoud uitrekenen? Als grondvlak kwam ik uit op: 1/4a≤√3. Hoe reken je dan 1/2a√3∑1/4a≤√3∑1/3 uit? Klopt het dat dit 1/12a≥√3 wordt? Alvast heel erg bedankt! 
Karin
Leerling bovenbouw havo-vwo - dinsdag 25 februari 2003
Antwoord

De lengte van de ribben van zo'n tetraŽder is a.
De vraag is dan:
1. Hoe bereken je de oppervlakte?
2. Hoe bereken je de inhoud?
Eerst maar eens een tekening:
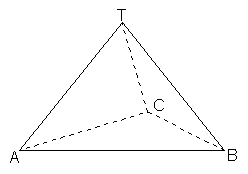
1.
Laten we eerst eens naar het 'grondvlak' ABC kijken:
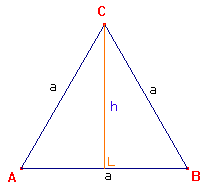
h=√(a2-(1/2a)2)=√(3/4a2)=1/2a√3
De oppervlakte van deze gelijkzijdige driehoek is dan:
Opp.=1/2∑a∑1/2a√3=1/4∑a2∑√3
Dus de oppervlakte van de tetraŽder is 4∑1/4∑a2∑√3=a2∑√3
..en dat is toch aardig...
2.
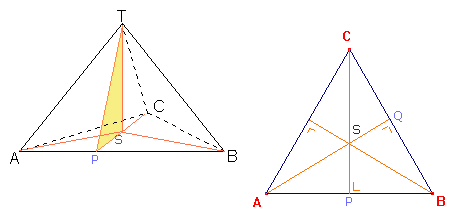
De hoogte h kunnen we berekenen in $\Delta$PST. PT=1/2a√3 (zie boven) en ST=h. Nu nog PS berekenen. Met behulp van het gegeven dat $\Delta$ABQ gelijkvormig is met $\Delta$ASP (ga na!) kan je PS berekenen.
PS=1/6∑a∑√3
h=√(PT2-PS2)=√((1/2a√3)2-(1/6a√3)2)=1/3a√6
Dus de inhoud van het tetraŽder wordt:
I=1/3∑1/4a2√3∑1/3a√6=1/12∑a3∑√2

|
Vragen naar aanleiding van dit antwoord? Klik rechts..!
donderdag 27 februari 2003
|

|



home |
vandaag |
bijzonder |
gastenboek |
statistieken |
wie is wie? |
verhalen |
colofon
©2001-2024 WisFaq - versie 3
|














