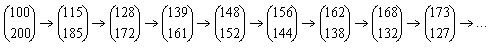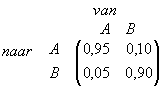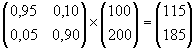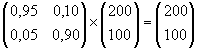Overgangsmatrix
In een dorp zijn twee winkels A en B. Elke maand zijn er klanten van winkel A die de volgende maand naar winkel B gaan. Andersom komt ook voor. Er zijn ook klanten die 'gewoon' bij hun oude winkel blijven.
Hiernaast zie je een graaf die deze situatie weergeeft.
Het getal 0,1 bijvoorbeeld betekent dat één tiende deel van de klanten van B de volgende maand gaat winkelen bij A.
Het getal 0,9 is het deel van de klanten van B die bij B blijft.Laten we eens uitgaan van de situatie dat A 100 klanten heeft en B 200. Dan heeft A één maand later 115 klanten en B heeft 185 klanten.
(ga maar na!)
Hieronder zie je wat er elke keer na een maand gebeurt:
Zoals je ziet neemt het aantal klanten van winkel A toe en neemt het aantal klanten van B neemt af. Het totaal aantal klanten verandert niet.
Ook kun je zien dat zowel de afname als de toename afneemt. Dit zou er op kunnen wijzen dat hier sprake is van een soort limietproces. Uiteindelijk zal het aantal klanten per winkel niet meer veranderen.Uiteindelijk heeft winkel A 200 klanten en B heeft er 100.
We kunnen bij deze situatie de volgende matrix maken:
We noemen zo'n matrix een overgangsmatrix. Let op de plaats van 'van' en 'naar'.
Met deze matrix kun je van een kolommatrix steeds de overgang naar de volgende maand uitrekenen:
Uiteindelijk ontstaat er een stabiele verdeling die je makkelijk kunt controleren door op die stabiele verdeling nog een keer de matrix toe te passen:
F.A.Q.



©2004-2024 WisFaq