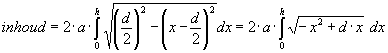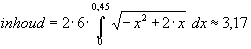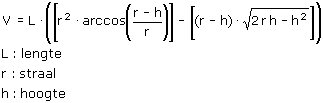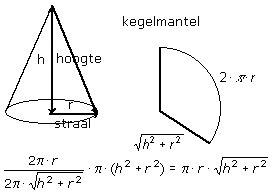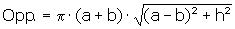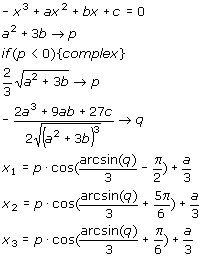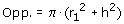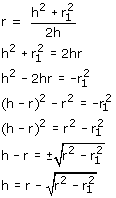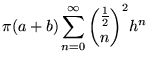Formules voor cirkel, bol, cilinder en nog wat...
- Cirkel, bol en cilinder
- Inhoud van een horizontale cilinder
- Inhoud en oppervlakte vergelijken
- Oppervlakte kegel
- Oppervlakte van de mantel van een afgeknotte kegel
- 'Wortelformule' voor derdegraads vergelijkingen?
- De abc-formule
- Bolkap
- Brekingswet van Snellius
- Omtrek en oppervlakte van een ellips
- Oppervlakte cirkelsegment
- FAQ's
Cirkel, bol en cilinder
Cirkel:
Omtrek=$2\pi r$
Oppervlakte=$\pi r^{2}$Bol:
Oppervlakte=$4\pi r^{2}$
Inhoud=$\frac{4}{3}\pi r^{3}$Cilinder:
Oppervlakte=$2\pi rh+2\pi r^{2}$
Inhoud=$\pi r^{2}h$
Inhoud van een horizontale cilinder
We nemen een horizontaal geplaatste cilinder met een doorsnede van d cm en een lengte van a cm. Het vloeistofnivo staat op een hoogte van h cm. Hoeveel vloeistof zit er nu in de cilinder?
Voorbeeld
Neem d=2, a=6 en h=0,45 dan:
Met de Ti83 kan je dit benaderen met de functie fnInt:
12*fnInt(V(-x2+2x),x,0,0.45)=3.174552221Horizontale cilinder (2)
Een andere formule voor de inhoud van een horizontale tank is:
De R-index
"Is er een formule te bedenken voor de effectiviteit van verpakkingen?"
Zie Effectiviteit van verpakkingen.
Oppervlakte kegel
"Hoe bereken je oppervlakte van een kegel?"
Zie Afleiden van de formule voor de oppervlakte kegel.

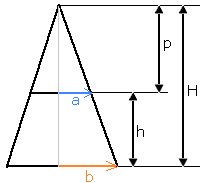
Oppervlakte van de mantel van een afgeknotte kegel
"Hoe bereken je oppervlakte van de mantel van een afgeknotte kegel?"
'Wortelformule' voor derdegraads vergelijkingen
"Bestaat er niet een soort 'abc-formule' voor derdegraads vergelijkingen?"
Zo eenvoudig als bij tweedegraads vergelijkingen zal het gaan. Hieronder staat de oplossing voor de vergelijking -x3+ax2+bx+c=0. Uiteraard kun je elke derdegraadsvergelijking omwerken tot deze vorm.
In de formule staat if(p<0){complex}. Dit betekent dat de oplossingen complex zijn.

De abc-formule
Voor een tweedegraads vergelijking van de vorm:
ax2 + bx + c = 0
kun de oplossingen uitrekenen met:
Zie abc-formule

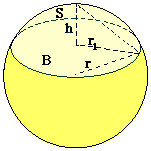
Bolkap
Oppervlakte
Inhoud
De hoogte bij gegeven r en r1
Zie ook Volume bolkap
Brekingswet van Snellius
De invallende lichtstraal en de uittredende lichtstraal/gebroken straal liggen in hetzelfde vlak. De specifieke brekingsindex (die voor iedere combinatie van stoffen anders is) is constant:
$\eqalign{\frac{\sin i}{\sin r}=constant=n}$
Hierin:
i = hoek van inval
r = hoek van breking
n = brekingsindex (zie binas)Bij overgang van een optisch 'dichtere' naar optisch 'minder dichte' stof (vb. water $\to$ lucht) vindt breking van de normaal af plaats. Lichtstralen zijn omkeerbaar dus van lucht naar water breekt licht naar de normaal toe. De grenshoek is de hoek van inval waarbij de hoek van breking 90 graden is. De grootte van de grenshoek volgt uit:
$\eqalign{\sin{g}=\frac{1}{n}}$
Hierin:
g = grenshoek
n = brekingsindex
Omtrek en oppervlakte van een ellips
De oppervlakte van een ellips kan je berekenen met de formule:
Opp(ellips)=$\large\pi$·a·b
Hierin zijn a en b de 'stralen' van de ellips (zie tekening). Als a=b gaat de formule over in:
Opp(cirkel)=$\large\pi$·r2
De omtrek is een heel ander verhaal. Er bestaat geen eenvoudige formule om exact de omtrek van een ellips te berekenen. Op MathWorld@Ellipse kan je lezen dat de berekening van de omtrek te maken heeft met elliptische integralen van de tweede soort.
Op de website geven ze ook een manier om de omtrek te benaderen met een reeks:
Voor benaderingen van de omtrek kan je volgende formules gebruiken:
$
\eqalign{
& {\text{Omtrek}} \approx \pi \sqrt {2(a^2 + b^2 )} \cr
& {\text{Omtrek}} \approx \pi \left[ {3(a + b) - \sqrt {\left( {a + 3b} \right)\left( {3a + b} \right)} } \right] \cr
& {\text{Omtrek}} \approx \pi \left( {a + b} \right)\left( {1 + \frac{{3h}}
{{10 + \sqrt {4 - 3h} }}} \right) \cr}
$
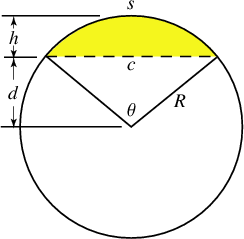
Oppervlakte cirkelsegment
Er is een vrij lastige formule af te leiden als R en h bekend zijn.
De laatste formule geeft een redelijke benadering als c en h bekend zijn.Zie Bron
FAQ's



©2004-2024 WisFaq