WisFaq!

De vraag was 'Hoeveel diagonalen heeft een zeshoek?' Wel aan... een plaatje dan maar?

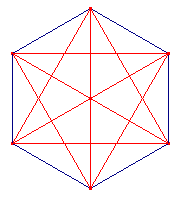
De rode lijnstukken zijn de diagonalen en dat zijn er negen!
Ik weet niet waar de nummers vandaan komen, maar we horen het wel...

Lukt dat zo?

Definitie
Een diagonaal van een veelhoek is een lijnstuk van hoekpunt naar hoekpunt die geen zijde is.
WvR
25-4-2024

Omtrek

Als je 4 bij 5 meter hebt wat is de omtrek dan?

Cato t
20-5-2024

Antwoord

Als het gaat om een rechthoek van 4 bij 5 meter dan is de omtrek gelijk aan 18 meter. Twee keer de lengte en twee keer de breedte.
Helpt dat?
WvR
20-5-2024

Re: Cirkels in een cirkel

De link http://www.enchantedlearning.com/tracing/circles2/circles.GIF werkt niet
Gerard
9-6-2024

Antwoord

Ik zag geen problemen!

Helpt dat?
WvR
9-6-2024

Hoeveel cirkels gaan er in een ring van cirkels

hoeveel kleine cirkels kunnen er maximaal (genest of liniair) in een ronde band van een grote cirkel
Gerard
9-6-2024

Antwoord

Hallo Gerardus,

Er is (naar mijn weten) geen formule die direct antwoord op jouw vraag kan geven. Wel kunnen we een benadring geven, en zeker een bovengrens (dus: een getal waar het aantal cirkels zeker onder zal liggen).
Wanneer we een heel grote ruimte met cirkels vullen, dan is de geneste rangschikking (zoals jij dit noemt) het meest efficiënt, zie de linker figuur hieronder:

Het gehele vlak kunnen we verdelen in gelijkzijdige driehoeken. Als we uitgaan van cirkels met straal=1, dan zijn de zijden van de driehoeken 2. De oppervlakte van zo'n driehoek is dan √3 $\approx$ 1,73. Binnen zo'n driehoek past 3 keer ¹/₆ deel van een cirkel, dus in totaal de helft van een cirkel. De oppervlakte hiervan is ¹/₂·$\pi$·1² $\approx$ 1,57. De cirkels bedekken dus ^1,57/_1,73·100% $\approx$ 91% van de totale oppervlakte.
In de rechter figuur zie je dat het vlak opgedeeld kan worden in vierkanten met zijde=2, waarin steeds één cirkel met straal=1 past. De oppervlakte van zo'n cirkel is $\pi$·1² $\approx$ 3,14, de oppervlakte van het omhullende vierkant is 2·2=4. De cirkel bedekt ^3,14/₄·100% $\approx$ 79% van de oppervlakte.
Conclusie: in een (oneindig) groot vlak kan je met de geneste rangschikking de meeste cirkels kwijt.

Wanneer de oppervlakte beperkt is, dan is niet automatisch de geneste rangschikking het meest efficiënt. Zie bijvoorbeeld het vierkant hieronder met zijde=4, waarin je zoveel mogelijk cirkels met straal=1 plaatst:

In de geneste opstelling is maar plaats voor 3 hele cirkels. De grijs gekleurde delen van volgende cirkels tellen niet mee, want we willen alleen hele cirkels kwijt. We halen dus nu niet meer 91% van de oppervlakte. In dit geval is de geneste opstelling beter, zie de rechter figuur. Met deze rangschikking passen 4 hele cirkels.

Bij grotere, maar beperkte oppervlakken kan het nog lastiger worden. Neem bijvoorbeeld een vierkant met zijden=10. Hierin plaatsen we zoveel mogelijk cirkels met diameter=1.
In de linker figuur hieronder zie je dat in de 'lineaire' rangschikking 10 rijen van 10 cirkels in het vierkant passen, dus 100 cirkels:

In de rechter figuur zie je dat in de geneste rangschikking 6 rijen van 10 cirkels en 5 rijen van 9 cirkels passen, dus in totaal 105 cirkels. De geneste opstelling is dus meer effeciënt.
Maar boven de stapel cirkels is nog wat ruimte over. Hierdoor kunnen de drie bovenste rijen ook recht boven elkaar worden geplaatst, hiermee krijgen we 7 rijen van 10 cirkels en 4 rijen van 9 cirkels, dus in totaal 106:

Hier is dus een 'gemengde' rangschikking het meest efficiënt.

In jouw geval hebben we te maken met gekromde randen van de beschikbare oppervlakte. Dan wordt het nog lastiger om de meest efficiënte rangschikking van cirkels te vinden, en dus het maximum aantal cirkels te vinden dat past. Wel kan je een absolute bovengrens berekenen:
Bereken de oppervlakte van de beschikbare ruimte (oppervlakte buitencirkel - oppervlakte binnencirkel;
Neem van deze oppervlakte 91% (dit is het grootst mogelijke percentage dat met cirkels bedekt kan worden);
Deel deze uitkomst door de oppervlakte van een enkele kleine cirkel, en rond naar beneden af op gehelen (dit heet 'afkappen')
Dit aantal is het grootst mogelijke aantal cirkels dat in de gegeven oppervlakte kan passen. Dit is wanneer de geneste opstelling precies in de gegeven ruimte past.
Zie voor een vergelijkbaar probleem de vraag Cirkels in een rechthoek, als reactie op deze vraag.
GHvD
19-6-2024

Omtrek van driehoek berekenen

Hallo
In driehoek ABC is AB=1 en BC = geheel getal. De bissectrice van A staat loodrecht op de zwaartelijn uit B. Bereken de omtrek van ABC.
M = snijpunt bisssectrice met BC.
AB/AC = BM/MC $\to$ AC = MC/BM
?
bedankt.
raf
10-7-2024

Antwoord

Hallo Raf,

Teken (het begin van) driehoek ABC, met de bissectrice van A en de zwaartelijn uit B, zie de figuur hieronder. Deze bissectrice en zwaartelijn snijden elkaar loodrecht in S.

De driehoeken ABS en AZS hebben 2 hoeken gemeen, en een gemeenschappelijke zijde AS. Deze driehoeken zijn dus gelijk. Dan is AZ=AB=1. daarmee wordt zijde AC=2.

Zijde BC is korter dan AB+AC, dus BC $<$ 3. Ook geldt: AC $<$ AB+BC, hieruit volgt BC $>$ 1. Omdat BC een geheel getal is, kan alleen gelden: BC=2. Hiermee kan je de tekening afmaken en de omtrek gemakkelijk berekenen:

GHvD
12-7-2024

Volume tetraëder

Dag

Ik moet het volume van een tetraëder met ribbe 4 cm berekenen via de formule: V= 1/3.grondoppervlakte.hoogte.
De grondoppervlakte heb ik kunnen vinden en is 6.9282 cm².
Voor de hoogte kom ik op 3 cm uit of 3.6, maar blijkbaar moet het 3,266 zijn. Ik gebruik Pythagoras. Grondvlak = ABC. S is voetpunt van de hoogte van de tetraëder met F als top. In driehoek ASF: FS² = BF² - AS² = 16 - 3 = $>$ FS = 3.6 cm.
Als ik een lijn trek van B naar S, dan in driehoek BSF: FS² = BF² - BS² = 16 - 7 = 9 en dus is FS = 3.
Geen enkele oplossing klopt.
Bedankt op voorhand.
Valerie.

Valeri
25-7-2024

Antwoord

Hallo Valerie,

Je aanpak is goed. De oppervlakte van het grondvlak is inderdaad 6,9282 cm². Hieronder heb ik het grondvlak getekend, met het voetpunt S van de top van de tetraëder:

De afstand AS is ²/₃ van de hoogtelijn AP. Met Pythagoras bereken je:

AP² = AB²-PB²
AP² = 4²-2²
AP = √12 = 3,4641

Dus:

AS = ²/₃·3,4641 = 2,3094

Bekijk dan driehoek ASF (waarin SF de hoogte van de tetraëder is):

Met Pythagoras bereken je:

FS² = AF²-AS²
FS² = 4²-2,3094²
FS = 3,2660.

Voor het volume V van de tetraëder vind je dan:

V = ¹/₃·6,9282·3,2660
V = 7,542 cm³

OK zo?
GHvD
25-7-2024