WisFaq!

Hier is een plot van $y=3x-\ln(6x)$ met daarbij $y=3x$ en $y=2x$,
en ook $y=(3-\frac6e)x$.

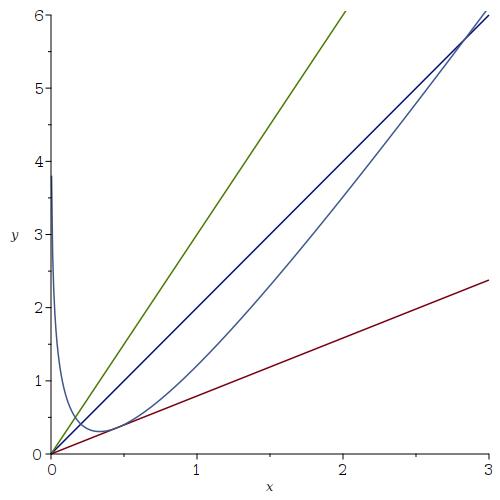
Dat illustreert dan je precies één snijpunt hebt als $a\ge3$ want dan geldt na het snijpunt links van $\frac16$ dat $ax\ge 3x > 3x-\ln(6x)$, zodat er later geen snijpunten meer komen.

Verder: als $a < 3$ dan kun je $a=3-b$ schrijven met $b > 0$. Dan hebt je te maken met $3x-bx$ en $3x-\ln(6x)$. Dan krijg je later nog een snijpunt, mits $b$ niet al te groot is. Als $b$ groter wordt krijgen we $bx > \ln(6x)$ voor alle $x$ en dus helemaal geen snijpunt.
Er is één $b$ waarbij de lijn raakt. Dat gebeurt als $y=bx$ aan $y=\ln(6x)$ raakt. Dus als $bx=\ln x + \ln6$, en tegelijk $b=\frac1x$. Vul $x=\frac1b$ in, dat geeft een vergelijking voor $b$, namelijk $1=-\ln b+\ln 6$, en dus $b=6/e$.

Dus één snijpunt als $a\ge3$, twee als $3\ge a > 3-\frac6e$, een raakpunt als $a=3-\frac6e$ en geen snijpunt als $3-\frac6e > a$.

kphart
15-2-2024