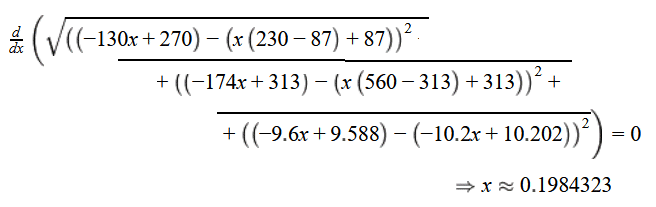WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Lineaire algebra

Ellips

Op een ellips E met brandpunten F,F' en met middelpunt O neemt men een punt D. Bewijs dat de volgende rechten concurrent zijn: de raaklijn t in D aan E, de loodlijn uit F op t, de evenwijdige door O met DF'. Als je dan de drie vglk zoekt moet de det dan 0 zijn en zoja waarom?

PVN
7-1-2025

Antwoord

Hallo,

De drie vergelijkingen van deze rechten kun je inderdaad schrijven in een stelsel van 3 vergelijkingen met (slechts) 2 onbekenden. In de meeste gevallen heeft zo'n stelsel geen oplossing. De voorwaarde dat het stelsel een oplossing heeft (d.w.z. de rechten hebben één gemeenschappelijk punt) is dat de determinant van de verkregen matrix gelijk is aan 0.
Men noemt dit algemeen het elimineren van n onbekenden uit n+1 (eerstegraads)vergelijkingen.

Ok?

LL
7-1-2025

Re: Ellips

Maar als de det=0 is het toch ofwel vals ofwel onbepaald,...
pvn
7-1-2025

Antwoord

Ik weet niet hoe ver jij op de hoogte bent van het bespreken van stelsels en de begrippen rang van een matrix en van de uitgebreide matrix van stelsels.
Ik zal het proberen uit te leggen zonder deze begrippen.

We gaan ervan uit de vergelijkingen lineair onafhankelijk zijn, dit wil zeggen dat de vergelijkingen geen veelvouden zijn en een vergelijking niet kan geschreven worden als een lineaire combinatie van andere vergelijkingen.
In jouw toepassing is dat zeker het geval.

Als we dan evenveel onbekenden als vergelijkingen hebben is er altijd precies één oplossing (1).
Als er één vergelijking meer is, is er algemeen geen oplossing meer want de kans is klein de gevonden oplossing in (1), ook past in de bijkomende vergelijking.
Er is dan enkel een oplossing als deze bijkomende oplossing een lineaire combinatie is van de andere vergelijkingen, en dan moet de determinant gelijk zijn aan 0.
Men noemt dit algemeen het elimineren van n onbekenden uit n+1 (eerstegraads)vergelijkingen.

LL
7-1-2025

Bewijs associativiteit groepentheorie

Ik wil bewijzen dat de viergroep van Klein een groep is. Voorbeeld {1,a,b,c}
Moet ik dit bij de voorwaarde associativiteit voor alle mogelijke combinaties doen? Of is 1 voorbeeld voldoende?
Moet ik dus als volgt
1*(a*b)=1*c=c net als (1*a)*b=a*b=c
EN 1*(1*1)=1*1=1 net als (1*1)*1=1
EN bewijzen dat (a*a)*a=a*(a*a)
EN a*(b*c)=(a*b)*c
Enz....?
Dat lijkt me toch enorm veel schrijfwerk. Hoe wordt dat normaal gedaan? Er zijn toch wel heel veel combinaties.... Je kan ook niet gewoon verwijzen naar de Cayley-tabel...

Tom
9-2-2025

Antwoord

Ja, als je niets anders hebt dan de groepstabel zul je alle drietallen langs moeten lopen.

Als alternatief kun je proberen die groep als symmetriegroep van een figuur te zien (een rechthoek die geen vierkant is); of als ondergroep van een andere groep, bijvoorbeeld $\bigl\{(1), (1\,2)(3\,4), (1\,3)(2\,4),(1\,4)(2\,3)\bigr\}$ als deel van $S_4$.
kphart
9-2-2025

Samennemen

Hallo als je 3 matrices hebt en dus 3 stelsels met 3 keer dezelfde coefficientenmatrix waarom mag je dat dan samennemen tot 1 matrix?
Karel
11-3-2025

Antwoord

Omdat je bij het oplossen van de drie stelsels drie keer dezelfde rijoperaties in de coëfficiëntenmatrix doet; dus die kun je net zo goed één keer doen voor alledrie stelsels tegelijk.
kphart
12-3-2025

Basis

Hallo, ik ben nu bij mijzelf basissen aan het leren, maar ik breek me over deze:

Stel een basis op voor
Span( (1,0,1,0),(1,2,1,-1),(-2,0,3,2),(0,0,5,2) )

Mvg Johan
Johan
19-3-2025

Antwoord

Kijk of een van de vier een lineaire combinatie van de andere drie is.
Zo nee: de vier zijn lineair onafhankelijk en vormen een basis.
Zo ja: laat die vector weg uit je viertal en herhaal het proces voor de
overige drie: is eentje een lineaire combinatie van de andere twee?
Zo nee: klaar, de drie vormen een basis.
Zo ja: doe die vector weg en kijk naar de overgeleven twee $\dots$
kphart
20-3-2025

Kortste afstand berekenen

Ik krijg een ander antwoord dan de uitwerking van het boek. Ik heb zelf gekeken of ik een verkeerde denkstap heb genomen, maar mij lijkt dat wat ik heb gedaan ook tot het juiste antwoord moet leiden.

De eerste stap, de ruimtevectoren van de vliegtuigen van mij zijn gelijk aan die van de uitwerkingen. Wat anders is, is dat in de uitwerkingen een vergelijking van een vlak wordt opgesteld en daarmee de afstandsformule wordt gebruikt. Ik heb de (naar 3D uitgebreide) formule van Pythagoras gebruikt en de afgeleide daarvan gelijk gesteld aan 0. Het tijdstip waarop de afstand dan minimaal is, is dan dit berekende tijdstip. Daarna heb ik dit tijdstip weer ingevuld in de gemaakte 'Pythagoras-formule' en daarmee de afstand verkregen.

Hieronder mijn uitwerking beknopt overgetypt:

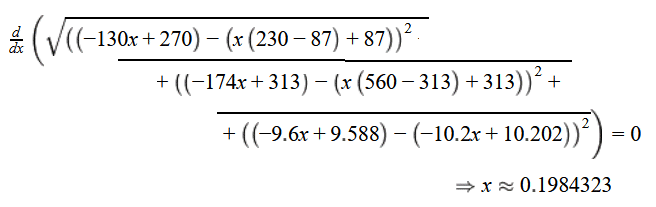
Die x weer invullen geeft ongeveer 153 544 meter als afstand en dat is veel meer dan wat er in de uitwerkingen staat. Wat klopt er niet aan mijn uitwerking?
Henk
20-3-2025

Antwoord

Lees de vraag nog eens goed: er wordt gevraagd naar de kortst mogelijke afstand tussen de twee vliegtuigen. Wat er niet staat is ook belangrijk, er staat niet dat de vliegtuigen tegelijk uit Brussel/Bonn vertrekken, noch dat ze dezelfde snelheid hebben; allemaal dingen die je wel in je uitwerking hebt gestopt.

De opgave vraagt op een nogal omslachtige manier naar de afstand tussen de twee lijnen waarlangs de vliegtuigen vliegen; dichter dan die afstand kunnen ze niet bij elkaar komen, ongeacht snelheid, startijd, enzovoort. De uitwerking die je beschrijft is correct: een vlak door de ene lijn parallel aan de andere opstellen en dan de afstand van de andere lijn tot dat vlak bepalen.
kphart
20-3-2025

Re: Basis

En hoe kan je snel bepalen of er een lineair afhankelijk is?
Ofwel kan je het gewoon zien en als je dit niet ziet, wat kan je dan doen. Want ik heb de det uitgerekend en die was natuurlijk 0 dus ze waren lineair afhankelijk en hoe weet ik dan welke kolom ik moet schrappen?

Mvg Johan
Johan
20-3-2025

Antwoord

Het hangt allemaal van je voorkennis af, maar in het algemeen kun je niet gewoon zien welke kolom je weg kunt laten. Je zult moeten rekenen. Ik heb al uitgerekend dat de vierde vector een lineaire combinatie van de eerste drie is door een stelsel vergelijkingen op te stellen via

$x_1(1,0,1,0)+x_2(1,2,1,-1)+x_3(-2,0,3,2)=(0,0,5,2)$:
$$\begin{cases}
x_1+x_2-2x_3=0\\
2x_2=0\\
x_1+x_2+3x_2=5\\
-x_2+2x_3=2
\end{cases}
$$Dus de vierde vector kan weg. Door nog drie van dit soort pogingen zul je zien dat de overige drie lineair onafhankelijk zijn. Als je al wat meer weet kun je dat al aan de oplossing van het stelsel zien.
kphart
21-3-2025

Re: Re: Basis

Dus een basis die slechts een deelruimte van gans R4 voortbrengt zijn dus deze koppels zonder de vierde? Zou je ook een beredeneerde gok kunnen doen door naar de determinant te kijken om zo te bepalen welke weg kan.
Johan
21-3-2025

Antwoord

Dat lijkt me niet, de determinant is maar één getal, en als die gelijk is aan $0$ dat zegt dat alleen maar dat de vier lineair afhankelijk zijn. Aan die nul kan ik niet zien welke vector (of vectoren) ik weg kan laten.
kphart
21-3-2025