WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Complexegetallen

Complexe getallen

Hoeveel complexe getallen z=a+bi voldoen aan:
|z³| = |z| en |z+1+i|= 1+√2?
De antwoordmogelijkheden zijn 0, 1, 2 en oneindig veel
Lou
13-1-2024

Antwoord

Maak een plaatje

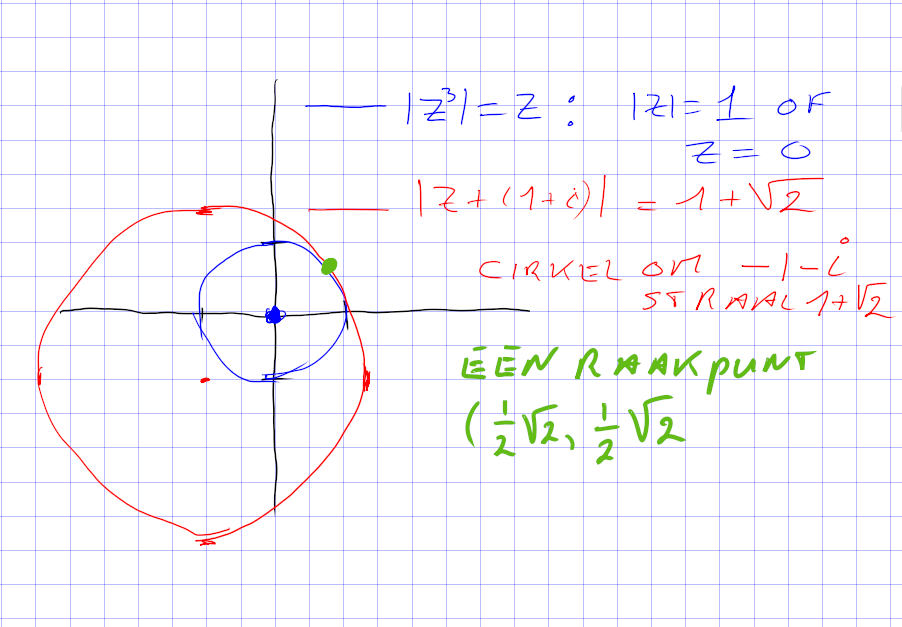
Je ziet één punt dat aan beide eisen voldoet.
kphart
14-1-2024

Complexe functie tekenen

hallo ik zoek een simpele aanpak om bijgevoegde functie te tekenen en plotten via een programma wat niet al te ingewikkeld is ( ik weet bijvoorbeeld dat het in MAtlab kan maar daar ben ik niet mee bekend). Wellicht dat iemand me hiermee kan helpen.
Gijs
14-2-2024

Antwoord

Wolfram Alpha is niet slecht.

Ik heb even gekeken en, ervanuit gaande dat $\Omega$ een complex getal is, het ziet ernaar uit dat je je functie om moet schrijven in $x$ en $y$. Dus $\Omega=x+jy$ stellen en de uitdrukking uitwerken. Dan splitsen in reëel deel $R$ en imaginair deel $I$, en $|R+jI|=\sqrt{R^2+I^2}$ uitwerken. Dan moet je ook je constanten $\zeta_1$ en $k_{12}$ kiezen, want anders komt er niets uit de plot.
kphart
14-2-2024

Re: Complexe functie tekenen

ik kom dan op
x^3+jxy^2-4x^2y-yx^2+y^3-2jxy...maar dan moet ik breuksplitsen
Gijs
15-2-2024

Antwoord

Dat lijkt me niet goed want $\Omega^4$ levert ook nog eens $x^4+4jx^3y-6x^2y^2-4jxy^3+y^4$.

Ik heb Maple te hulp geroepen en die geeft, voor de uitdrukking in $\Omega$:
$$
R(x,y)=1+x^{4}-6 x^{2} y^{2}+y^{4}-\left(4 \zeta^{2}+2 k +2\right) \left(x^{2}-y^{2}\right)+k +4 \zeta \left(3 x^{2} y -y^{3}\right)-4 \zeta k y -4 \zeta y
$$
en
$$
I(x,y)=4 x^{3} y -4 x \,y^{3}-2 \left(4 \zeta^{2}+2 k +2\right) x y -4 \zeta \left(x^{3}-3 x \,y^{2}\right)+4 \zeta k x +4 \zeta x
$$
(ik heb de indices aan $\zeta$ en $k$ even weggelaten).
De functie die je wilt plotten wordt dan
$$
k*\bigl(R(x,y)^2+I(x,y)^2\bigr)^{-\frac12}
$$
Daar zou wolfram alpha geen problemen mee moeten hebben.

Ik heb ontdekt dat Maple precies doet wat je wilt, definieer
$$
f(z)=z^{4}-4 \,j \zeta \,z^{3}-2 \left(2 \zeta^{2}+k +1\right) z^{2}+4 \,j \zeta \left(1+k \right) z +1+k
$$
($z$ in plaats van $\Omega$).
Het commando
complexplot3d(g(z), z=a+b*I..c+d*I);
geeft een plot van de modulus van de gegeven functie $g(z)$ over de rechthoek tussen $a+bj$ en $c+dj$.

Dus wat jij moet hebben krijg je met
complexplot3d(k/f(z), z=a+b*I..c+d*I);
Hier is een voorbeeld met $\zeta=k=1$ en $z=(0.1+0.1j)\, ..\, (1+j)$

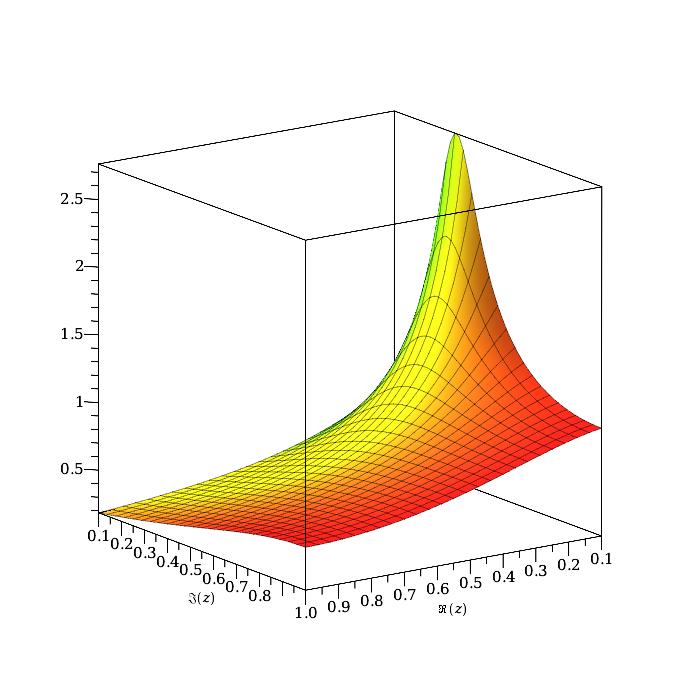
kphart
15-2-2024

Re: Re: Complexe functie tekenen

wow! dat ziet er goed uit...ik ga ernaar kijken ....ps het klopt dat ik niet alle $\Omega $ termen heb uitgewerkt enkel de j $\Omega $ , dit is een formule over trillingen en $\Omega $ staat voor de verhouding van de frequentie : $\omega $ / $\omega $ n ...de j staat toch voor het imaginaire deel ( faseverschuiving)?
Gijs
16-2-2024

Antwoord

Dat kan zijn, maar in je vraag staat de modulus van de hele complexe functie en daar spelen het reële en het imaginaire deel allebei een rol.

kphart
16-2-2024

Riemann-zeta functie met complex getal als argument

Hoe kun je $\zeta $ (x) berekenen wanneer x $\in $ $\mathbf{C}$ ? En waarom denkt men dat alle non-triviale nulpunten op ¹/₂+bi liggen?
Oliver
12-4-2024

Antwoord

Een volledig antwoord is niet binnen het bestek van de wisfaq te geven.

De link hieronder verwijst naar een boekje over de Riemann-hypothese waarin alles rustig wordt uitgelegd.
Zie De Riemann-hypothese (Epsilon-reeks 69).

kphart
14-4-2024

Reëel en imaginair deel van complexe getallen berekenen

Ik heb een vraag over deze oefeningen:

a) z1= 1/i (mijn oplossing is dat het reëele deel 0 is en het imaginaire deel -1 maar ik ben hier niet zeker over)

b) z2= 1/1-i $\sqrt{}$ 3 (mijn oplossing: reëel= 1/4 imaginair= $\sqrt{}$ 3/4 maar ben hier ook niet zeker over)

c) z3=(-2+5i)·(1+3i)/2+3i - (2/13-3/13i) (ik weet niet goed hoe ik aan deze oefening moet beginnen)

Alvast bedankt voor de hulp!
Y
19-4-2024

Antwoord

a. $i^{-1}=-i$, dus dat klopt
b. $1/(1-i\sqrt3)=\frac14+\frac14i\sqrt3$, denk om de haakjes!
c. Ik weet ook niet hoe ik moet beginnen want ik zie niet goed hoe de haakjes zouden moeten staan; schrijf die nog eens ondubbelzinnig op.
kphart
19-4-2024

Re: Reëel en imaginair deel van complexe getallen berekenen

Nogmaals bedankt voor de moeite!
Y
23-4-2024

Antwoord

Complex delen doe je door teller en noemer met de complex toegevoegde van de noemer te vermenigvuldigen. De breuk in je som wordt dan
$$\frac{(-2+5i)\cdot(1+3i)\cdot(2-3i)}{(2+3i)\cdot(2-3i)}=
\frac{(-2+5i)\cdot(1+3i)\cdot(2-3i)}{13}
$$Nu de teller netjes uitvermenigvuldigen en dan nog de andere term aftrekken.

kphart
23-4-2024

Complexe eenheidscirkel

Hoe verklaar je met de eenheidscirkel in het complexe vlak, het kwadratische karakter van 2, dus (2/p) waarbij p een oneven priemgetal is.
jan
26-7-2024

Antwoord

Je kunt rekenen modulo $p$ ook in het complexe vlak uitvoeren: voor $k=1$, $2$, $\ldots$, $p-1$ heb je de complexe getallen $e^{k\frac {2\pi}p\mathrm{i}}$. Die liggen op de eenheidcirkel en vormen een regelmatige $p$-hoek die rechts begin in $1=e^{0\cdot\frac{2\pi}p\mathrm{i}}$, teken hem maar eens voor $p=3$, $p=5$ en $p=7$ (voor grotere $p$ gaat het ook wel maar het is meer werk).

Optellen modulo $p$ komt overeen met vermenigvuldigen van de complexe getallen:
$$e^{k\frac {2\pi}p\mathrm{i}}\cdot e^{l\frac {2\pi}p\mathrm{i}}=e^{(k+l)\frac {2\pi}p\mathrm{i}}
$$Vermenigvuldigen modulo $p$ is dan eigenlijk machtsverheffen:
$$e^{k\cdot l\frac {2\pi}p\mathrm{i}}=\bigl(e^{k\frac {2\pi}p\mathrm{i}}\bigr)^l = \bigl(e^{l\frac {2\pi}p\mathrm{i}}\bigr)^k
$$meetkundig vermenigvuldig je de hoek $k\frac {2\pi}p$ met $l$ (of andersom).

Dus $2$ is een kwadraat modulo $p$ als je een hoek $k\frac {2\pi}p$ kunt vinden die als je hem met $k$ vermenigvuldigt precies uitkomt op $e^{\frac{4\pi}p\mathrm{i}}$.
kphart
30-7-2024