Inversie in de vlakke meetkunde als bewijstechniek

Formulering van het probleem:

De rechte a, gaande door het vaste punt A, snijdt de vaste cirkel K₁(O, r) in de punten B en C. Cirkel (K₂) resp. (K₃) gaat door A en B resp. A en C en raken beide aan (K₁). Noem P het 2e snijpunt van (K₂) en (K₃). Toon aan dat P op de cirkel ligt gaande door A, D en O.

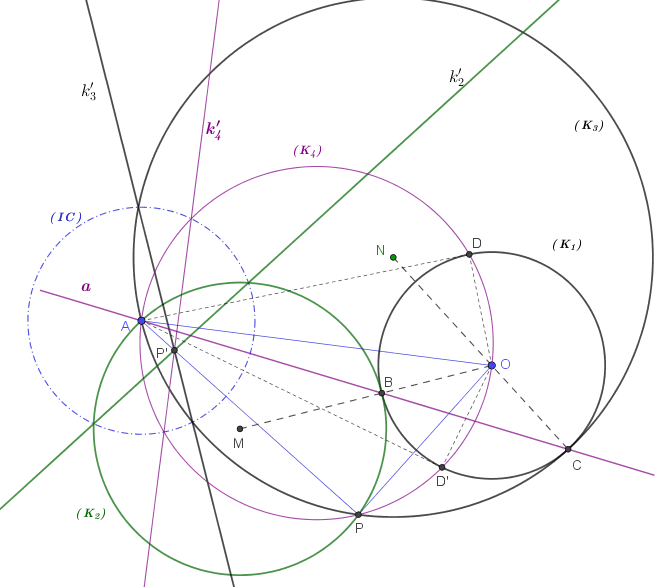
In de bijlage werd met GeoGebra een schets gemaakt van de situatie. Het middelpunt van (K₂) resp. (K₃) is M resp. N. Vervolgens werd de vierhoek ADOP getekend. Bij constructie is AD loodrecht op OD in D.

Ik koos dan voor de inversie (A, ?²), met centrum het punt A en inversiestraal ?. Daar (K₂) en (K-3) beide door A gaan worden ze omgezet in de rechten k'₂ en k'₃. Het snijpunt van die beide rechten noem ik P', en dat is tevens het beeld van P onder de inversie (A, ?²).

Vervolgens tekende ik een 4e cirkel (K₄) gaande door A, D en O en onderwierp deze aan de inversie (A,?²). Dit leverde de rechte k'₄ op want (K₄) gaat ook door het inversiecentrum.

Tezelfdertijd valt meteen op dat k'₄ door P' gaat. Daar P' het beeld is van P onder de inversie (A,?²), besluit ik hieruit dat P op de cirkel (K₄) moet liggen.

Mijn VRAAG: Is deze manier (zuiver visueel) van concluderen aanvaardbaar of niet? Of zou u hier opteren voor een andere aanpak? Indien deze vraag in aanmerking komt, had ik graag jullie mening hierover gekregen met al dan niet een tip om het anders te proberen. Bedankt bij voorbaat!

Yves D
Iets anders - maandag 11 oktober 2021

Antwoord

Beste Yves,

Over je vraag "Is deze manier (zuiver visueel) van concluderen aanvaardbaar of niet?" kunnen we kort zijn: neen.

Laat me je een tip geven voor dit lastige probleem:

Je kunt aantonen dat driehoeken $ANC$, $BOC$ en $AMB$ gelijkvormig zijn.
In het bijzonder is $AMON$ een parallellogram.
Dat betekent dat de middens van $AO$ en $MN$ samenvallen. Noem dat midden $Q$.
In het bijzonder zijn $M$, $N$ en $Q$ op één lijn gelegen.
Maar dat betekent dat de cirkels $(K_2)=(M,MA)$, $(K_3)=(N,NA)$ en $(K_4)=(Q,QA)$ een cirkelbundel vormen.
Behalve door $A$ gaan ze dus alledrie door $P$.

Met vriendelijke groet,

zaterdag 23 oktober 2021

©2001-2024 WisFaq