
Sinē2x omzetten naar algemene sinusfunctie
Ik heb een probleem om sin2x om te zetten naar algemene sinusfunctie.
Dit is wat ik heb:
sin2x
= sin2x . sin2x
= 4 . sin2x . cos2x
= 4 . 0,5 . (1-cos2x) . 0,5 . (1+cos2x)
= (1-sin(2x+$\pi$/2) . (1+sin(2x+$\pi$/2)
hoe moet ik nu verder om 1/2.sin[4(x+3$\pi$/8)]+1/2
Steven
3de graad ASO - zondag 30 maart 2008
Antwoord
Hallo
Je weet : sin2x = 1/2.[1-cos(2x)]
Dus : sin22x = 1/2.[1-cos(4x)] =
1/2.[1-sin($\pi$/2-4x)] (complementaire hoeken) =
1/2.[1+sin(4x-$\pi$/2)] (tegengestelde hoeken) =
1/2 + 1/2.sin[4.(x-$\pi$/8)]
(Deze uitdrukking is identiek aan je uitdrukking hierboven!)
Hieruit kun je dus verschuivingen, de uitrekking en periode afleiden.
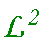
maandag 31 maart 2008
 ©2001-2024 WisFaq
©2001-2024 WisFaq
|