WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Analytisch bewijs meetkunde

ik zit vast bij mijn oefening:

'In een driehoek ABC trekt men de hoogtelijnen AD en BE (D BC en E AC). Het midden M van [AB] wordt met het midden N van [DE] verbonden. Bewijs analytisch dat MN loodrecht staat op DE.'

ik heb mijn driehoek zo geplaatst dat A(ax,ay),B(b,0),C(0,0) als co hebben.
Nu weet ik dat rico AC(ay/ax) tegenovergestelde is van BE [hoogtelijn]
(-ax/ay).
Om punt E te vinden stelde ik de vglen van AC en BE gelijk:
(ay/ax)x = (-ax/ay)(x-b), dan bekom ik voor x=(ax²*b)/(ay²+ax²) en voor co y van E: y=(-ax/ay)((ax²*b)/(ay²+ax²)-b)
co(M)=((ax+b)/2,ay/2)

vanaf hier loopt het mis. Ik probeer om de rico van ED te vinden maar ik kom verkeerd uit.

Kunt u me vertellen wat ik verkeerd heb gedaan of hoe ik dit misschien simpeler zou kunnen oplossen?

Alvast bedankt!

Alvast bedankt voor jullie hulp!
maxime
2de graad ASO - vrijdag 12 mei 2023

Antwoord

Hallo Maxime,

Dit lijkt me een nogal ingewikkelde aanpak. Ik zou het als volgt doen, zie onderstaande figuur:

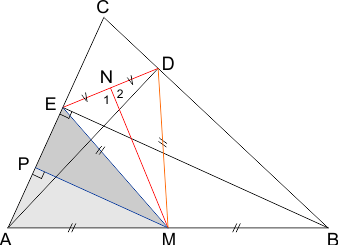
Gegeven driehoek ABC met hoogtelijnen AD en BE. N is het midden van ED. Te bewijzen is dat MN loodrecht staat op ED.

Teken de loodlijn MP vanuit M op AC. De driehoeken ABE en AMP zijn gelijkvormig (kan je zelf aangeven waarom dat is?). Omdat AM=MB geldt ook AP=EP. Zodoende zijn ook de driehoeken AMP en EMP gelijkvormig, dus EM=AM.

Op dezelfde wijze kan je aantonen dat DM=MB, dus geldt: DM=EM. Omdat EN=DN zijn de driehoeken EMN en DMN gelijk, dus hoek N₁=hoek N₂=90°.

Vragen naar aanleiding van dit antwoord? Klik rechts..!
zaterdag 13 mei 2023

Re: Analytisch bewijs meetkunde