|
|
|
\require{AMSmath}
Re: Re: Verhouding delen piramide in kubus
Beste
Ik weet niet hoe je de inhoud van die piramide die in twee stukje gedeeld is kan berekenen. We moeten de verhouding berekenen van de twee stukjes van die piramide maar ik weet niet hoe je de verhouding kan berekenen van 2 die twee figuren
mvg
Liesje
liesje
3de graad ASO - zondag 18 april 2021
Antwoord
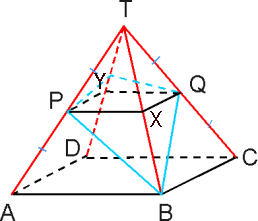
De inhoud van de hele piramide:
$
\eqalign{
& V_{groot} = \frac{1}
{3} \cdot G \cdot h \cr
& G = 16 \cr
& h = \sqrt {4^2 - \left( {2\sqrt 2 } \right)^2 } = 2\sqrt 2 \cr
& V_{groot} = \frac{1}
{3} \cdot 16 \cdot 2\sqrt 2 = \frac{{32}}
{3}\sqrt 2 \cr}
$
Bovendien:
$
\eqalign{
& V_{klein} = \frac{1}
{3} \cdot G \cdot h \cr
& G = 4 \cr
& h = \sqrt 2 \cr
& V_{klein} = \frac{1}
{3} \cdot 4 \cdot \sqrt 2 = \frac{4}
{3}\sqrt 2 \cr}
$
Dat is al iets...
|
Vragen naar aanleiding van dit antwoord? Klik rechts..!
zondag 18 april 2021
|
|
home |
vandaag |
bijzonder |
gastenboek |
statistieken |
wie is wie? |
verhalen |
colofon
©2001-2024 WisFaq - versie 3
|
Dit is een reactie op vraag 91955