WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Constante hoek tussen 2 snijdende cirkels

Opgave: Gegeven is een vast punt P niet gelegen op de cirkel K(O, r) en 2 vaste punten A en B wel gelegen op (K); eveneens is het punt M variabel op de cirkel (K). Toon dan aan dat de cirkels K₁(AMP) en K₂(BMP) elkaar onder een vaste hoek snijden als M zich verplaatst op K(O, r).

Mijn bevindingen: Deze opgave stond vermeld bij het hoofdstuk 'Inversie', dus is het toch de bedoeling dit met een gepaste inversie op te lossen.

Ter info: Ik kon het bewijs leveren door te steunen op de stelling dat hoeken die staan op een zelfde koorde van een cirkel, gelijk zijn.

Ik probeerde dit dan ook via een inversie en achtereenvolgens koos ik als inversiecirkel (IC) de cirkel (K), waar A, B en M zijn op gelegen (zie Fig. 1), en nadien, koos ik als inversiecirkel, de cirkel gaande door A, B en M (zie Fig. 2). Ik inverteerde telkens de raaklijnen in M aan beide cirkels (K₁) en (K₂) en bekwam de cirkels (K'₁) en (K'₂). De raaklijnen r'₁ en r'₂ in M (Fig.1)resp. in M' (Fig. 2) maken natuurlijk dezelfde hoek als de raaklijnen r₁ en r₂. Maar deze aanpak laat niet toe om aan te tonen dat die hoeken (tussen r₁ en r₂ enerzijds, en r'₁ en r'₂ anderzijds) constant blijven als M beweegt over K(O, r).

Ik twijfel er nu aan of deze oefening wel kan worden opgelost worden met een inversie. Van daar ook mijn vraag.

VRAAG: Is het hier zinvol om dit probleem via een inversie aan te pakken? Zo ja, kan u mij dan een tip geven hoe ik dat het beste oplos? Eventueel de inversiecirkel nog op een andere manier kiezen, dan ik deed in beide pogingen?

Bedankt voor uw tussenkomst!
Yves D
Iets anders - zaterdag 28 november 2020

Antwoord

Beste Yves,

Het duurde even voor ik hem zag, maar een oplossing met inversie gaat als volgt: Neem als inversiecirkel de cirkel met middelpunt $P$ die $(K)$ orthogonaal snijdt. Dan wordt $K$ afgebeeld op zichzelf, in het bijzonder kun je de beelden van $A$ en $B$ vinden als de punten $A'$ en $B'$ die het tweede snijpunt zijn van $PA$ en $PB$ met $(K)$. $A'$ en $B'$ zijn vaste punten.

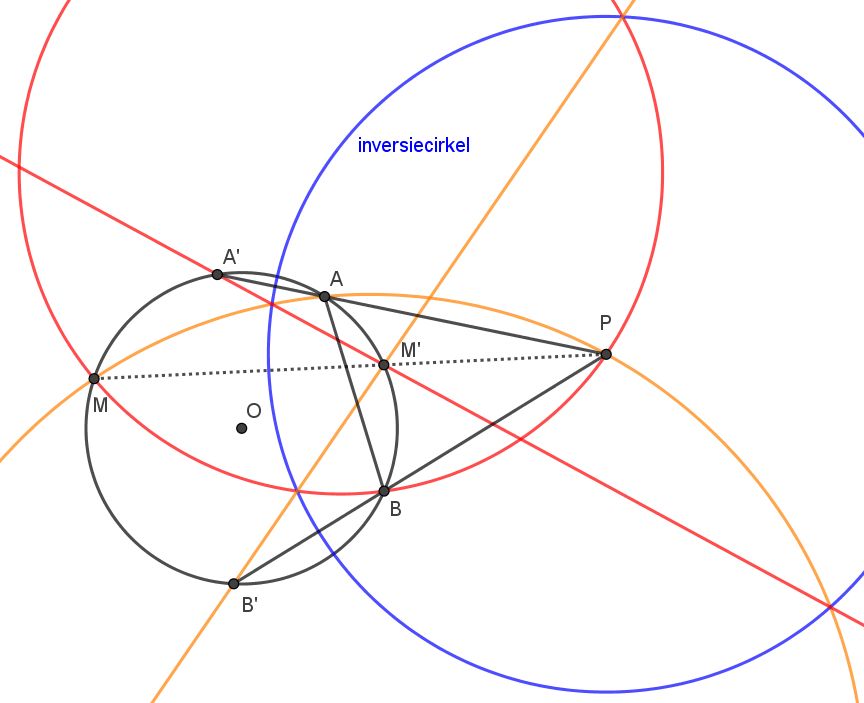
Het beeld $M'$ van $M$ is uiteraard ook het tweede snijpunt van $PM$ met $(K)$ en is een variabel punt. De beelden van $(K_1)$ en $(K_2)$ zijn $M'A'$ en $M'B'$. Vanwege de constante hoekstelling, $A'B'$ is een vaste koorde, is de hoek tussen $M'A$ en $M'B$ constant. Aangezien inversie de onderlinge hoek behoudt, betekent dit dat ook $(K_1)$ en $(K_1)$ elkaar onder een constante hoek snijden.

Met vriendelijke groet,

Vragen naar aanleiding van dit antwoord? Klik rechts..!
maandag 7 december 2020