|
|
|
\require{AMSmath}



Re: Re: Re: Co÷rdinaat van een punt
Ik heb geprobeerd om 2 keer d(B, C1) gelijk te stellen aan d(A, C1) aangezien de afstand van (B, C1) 2 keer groter is dan d(A, C1).
De co÷rdinaten van C2 heb ik gevonden met u hulp.
Alleen weet ik niet hoe ik verder moet om C1 te berekenen..
Mijn excuses alvast voor het storen.
Mvg
Tugce
3de graad ASO - woensdag 16 september 2020
Antwoord
Hallo Tugce,
Je hebt netjes gevonden:
d(B,P):d(A,Q) = 2:1
Dan geldt ook:
d(P,C1):d(Q,C1) = 2:1
en
d(YP:yC1)):d(yQ:YC1)) = 2:1, zie de figuur hieronder.
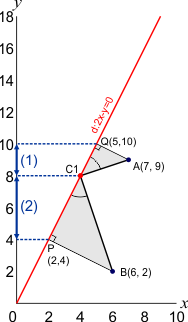
Om verder te kunnen werken, moeten we eerst de co÷rdinaten van P en Q berekenen. Voor P gaat dit als volgt:
De rechte d heeft als vergelijking d:2x-y=0. De lijn BP staat loodrecht op d, dan geldt voor BP:
x+2y=c
We weten dat deze lijn door B(6,2) gaat, dus:
6+2Ě2=c
c=10
Het punt P is het snijpunt van d en de lijn BP. We vinden P door dit stelsel op te lossen:
2x-y=0
x+2y=10
We vinden: P(2, 4).
Op overeenkomstige wijze vinden we: Q(5, 10)
We kunnen nu yC1 berekenen. In de figuur zie je:
yC1 = yP + 2/3(yQ-yP)
yC1 = 4 + 2/3(10-4)
yC1 = 8
Op gelijksoortige wijze kan je xC1 uitrekenen, maar sneller is omde gevonden waarde van yC1 invullen in de vergelijking van de rechte d:
2x-y=0
2xC1-8=0
xC1=4
dus: C1(4, 8).
Zijn hiermee de moeilijkheden opgelost? Zo niet: stel gerust een vervolgvraag, je hoeft geen excuses aan te bieden. We zijn er juist om jou met je wiskunde vooruit te helpen.

|
Vragen naar aanleiding van dit antwoord? Klik rechts..!
donderdag 17 september 2020
|

|



home |
vandaag |
bijzonder |
gastenboek |
statistieken |
wie is wie? |
verhalen |
colofon
©2001-2024 WisFaq - versie 3
|








 Dit is een reactie op vraag 90482
Dit is een reactie op vraag 90482 

