|
|
|
\require{AMSmath}



Re: Re: Co÷rdinaat van een punt
Misschien heb ik de vraag fout verwoord.
De vraag zoals het er letterlijk in staat: Men geeft de punten A(7,9) en B(6,2) en de rechte d:2x-y=0
Zoek de co÷rdinaten van de punten C gelegen op d zodat CA en CB gelijke hoeken maken met d.
Oplossing moet in de vorm van C1(...,...) en C2(...,...)
Mijn excuses voor het storen.
Mvg
Tugce
3de graad ASO - woensdag 16 september 2020
Antwoord
Hallo Tugce,
Nu is de vraag een stuk duidelijker. Je moet een punt C op de rechte vinden, zodanig dat de hoek tussen de lijn AC en de rechte gelijk is aan de hoek tussen BC en de rechte. Er zijn twee oplossingen, deze twee punten kan je C1 en C2 noemen. Hieronder heb ik de oplossingen getekend:
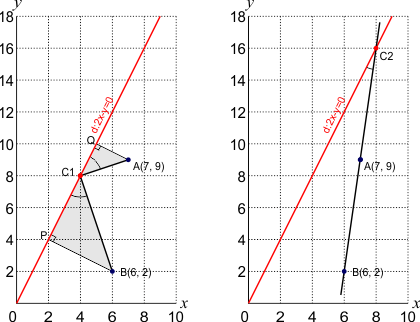
In de rechter figuur is C2 het snijpunt tussen de rechte d en de lijn AB. De hoek tussen de rechte en de lijn C2-A is natuurlijk gelijk aan de hoek tussen de rechte en de lijn C2-B, want het gaat om dezelfde hoek. Je vindt het punt C2 door het snijpunt te bepalen tussen de rechte d en de lijn AB.
Links heb ik C1 getekend, en de lijnen BP en AQ, beide loodrecht op d. De hoeken P-C1-B en A-C1-Q zijn gelijk, zoals gevraagd. Om het punt C1 te vinden, moet je beseffen dat de grijze driehoeken BPC1 en AQC1 gelijkvormig zijn (kan je dit aantonen?). Dan geldt:
PC1:QC1 = BP:AQ
Bereken dus de lengtes van BP en AQ, je kent dan de verhouding BP:AQ. Vervolgens verdeel je de afstand PQ in twee delen met dezelfde verhouding.
Kan je hiermee verder?

|
Vragen naar aanleiding van dit antwoord? Klik rechts..!
woensdag 16 september 2020
|

|



home |
vandaag |
bijzonder |
gastenboek |
statistieken |
wie is wie? |
verhalen |
colofon
©2001-2024 WisFaq - versie 3
|








 Dit is een reactie op vraag 90481
Dit is een reactie op vraag 90481 

