|
|
|
\require{AMSmath}



Pakket aan een touw verplaatsen dat rond een balk hangt
Oefening:
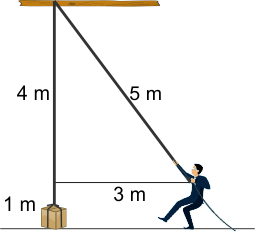
Kaat wil een pakket omhoog hijsen. Ze hangt hiervoor het pakket aan een touw dat rond een balk hangt. De balk hangt op 5 meter hoogte boven de grond en kan niet bewegen. In de beginsituatie ligt het pakket op de grond. Kaat houdt het touw strak gespannen vast op 1 meter boven de grond, en staat 3 meter rechts van het pakket. Daarna loopt ze naar rechts. Ze laat het touw niet los en blijft het touw op 1 meter hoogte houden. Het touw glijdt over de balk en het pakket schuift naar boven. Als Kaat 1 meter opgeschoven is naar rechts, welke van onderstaande waarden is dan de beste benadering voor de afstand waarover het pakket naar boven geschoven is? De dikte van de balk mag verwaarloosd worden t.o.v. de andere gegeven afmetingen. De figuur hieronder is een principetekening van de beginsituatie, de afmetingen zijn niet in de juiste verhoudingen getekend.
Mijn redenering:
Door de stelling van Pythagoras toe te passen kun je afleiden dat het touw tussen de persoon en de balk 5m is, maar weet niet precies of dit belangrijk is. I denk ook dat het om een exponentiŽle functie gaat. Wat ik ook denk is als de persoon op 8m (5+3) is de box om zijn maximum is. Het antwoord 0.65m is maar weet niet hoe ze hieraan komen. Zou iemand zo vriendelijk willen zijn om mij uit te leggen hoe dit vraagstuk in elkaar zit, en wat je moet doen om hem op te lossen.
Alvast Bedankt
D.
Duncan
3de graad ASO - maandag 20 juli 2020
Antwoord
Hallo Duncan,
Je hebt geen tekening meegestuurd, maar als ik de tekst goed lees, dan lijkt de situatie te zijn zoals ik in de figuur hieronder heb weergegeven. Je hebt op de juiste manier berekend dat het schuine stuk touw 5 meter lang is. Dit is ook belangrijk.
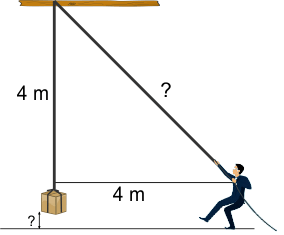
In de figuur hieronder heb ik de nieuwe situatie getekend: de persoon is 1 meter naar rechts opgeschoven. Het schuine stuk touw is nu langer. Met de stelling van Pythagoras kan je vast wel berekenen hoeveel langer dit stuk is geworden. Je weet dan ook hoeveel het pakket omhoog is gekomen.

|
Vragen naar aanleiding van dit antwoord? Klik rechts..!
maandag 20 juli 2020
|

|



home |
vandaag |
bijzonder |
gastenboek |
statistieken |
wie is wie? |
verhalen |
colofon
©2001-2024 WisFaq - versie 3
|











