WisFaq!

Loading jsMath...

De digitale vraagbaak voor het wiskundeonderwijs

HOME

\require{AMSmath}

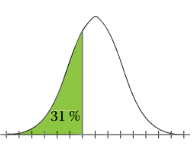
Normaalkromme

Als er om de normaalkromme een bepaalde oppervlakte is ingekleurd (percentage) hoe bereken je dan de ontbrekende grenzen? Ik dacht met Z-score maar gaat dit niet anders?

Timmy
3de graad ASO - zondag 14 juni 2020

Antwoord

Dat hangt af van het gemiddelde en de standaardafwijking.

Voor de standaard normale verdeling met \mu = 0 en \sigma = 1 kan je met een tabel of rekenmachine de bijbenorende z-score bepalen:
De normale tabel
m = s =
x <
P(x < ...) =
< x <

P(... < x < ...) =
z \approx {\rm{ - 0}}{\rm{,4959}}

Op De normale verdeling kan je zien het dan met mijn GR gaat.

Voor andere waarden van \mu en \sigma kan je bijbehorende grens berekenen. Gebruik daarvoor:

\eqalign{z = {{x - \mu } \over \sigma }}

Helpt dat?

Lesbrief normale verdeling
Van de 'oude' cursus statistiek 2-1 - 24 pagina's

Vragen naar aanleiding van dit antwoord? Klik rechts..!
zondag 14 juni 2020