|
|
|
\require{AMSmath}



Invloed van blauwe ogen op doofheid van katten
Beste,
Ik zit vast bij deze oefening:
Er gaat een hardnekkig gerucht dat de kans op doofheid bij een kat te maken heeft met de kleur van de ogen, maar volgens mij is dat niet waar. Nou is bekend dat in totaal 30% van alle katten blauwe ogen heeft. Een onderzoek onder 100 dove katten leverde op dat daarvan 38 katten blauwe ogen hadden.- Wat moet ik aan de hand van deze gegevens met α= 0,05 concluderen?
- Wat zal iemand die beweert dat katten met blauwe ogen vaker doof zijn dan andere katten aan de hand van deze gegevens met α= 0,05 concluderen?
Ik heb a al geprobeerd. Ik heb als H0 (=nulhypothese) p=0,3 (30% van de katten heeft blauwe ogen en 30% is ook de kans op doofheid. M.a.w. blauwe ogen hebben invloed op doofheid) en als Ha (alternatieve hypothese) p=/= 0,3 (blauwe ogen hebben geen invloed). Ik heb de p-waarde berekend en die is 0,0809. Daardoor mag ik de nulhypothese niet verwerpen en kunnen we concluderen dat blauwe ogen wel een invloed hebben op doofheid.
Ik ben onzeker van mijn oplossing en ik kan er niet mee verder gaan om b. op te lossen. Als iemand me kan helpen dan zal daar dankbaar voor zijn.
Mvg
Sara
3de graad ASO - woensdag 10 juni 2020
Antwoord
Hallo Sara,
Laten we even alles goed op een rijtje zetten. Allereerst: we starten altijd met de aanname dat er geen verschillen zijn, geen afwijkingen, geen invloed enz. In andere woorden: we nemen aan dat alle gevonden verschillen puur toevallig zijn. Dat is de nulhypothese. In dit geval is dit dus:
H0: blauwe ogen hebben geen invloed op doofheid (dus: proportie dove katten p=0,30)
Vervolgens berekenen we de kans dat gevonden resultaten door toeval ontstaan. Als die kans erg klein is, dan trekken we de conclusie dat de resultaten kennelijk niet puur toevallig zijn. We verwerpen dan alsnog de nulhypothese en nemen aan dat er toch wel invloed is tussen oogkleur en doofheid. Dit is de alternatieve hypothese:
H1: blauwe ogen hebben wel invloed op doofheid (dus: p$\ne$0,30)
Als de gevonden steekproefproportie alleen maar van toeval afhangt, dan zullen gevonden proporties normaal verdeeld zijn, zie de figuur hieronder. Wanneer de gevonden waarde in het rode gebied ligt, dan vinden we het onwaarschijnlijk dat alleen toeval in het spel is en gaan we ervan uit dat er toch een verband is. De grens ligt bij $\alpha$=0,05. Dat wil zeggen: de totale rode oppervlakte is 0,05.
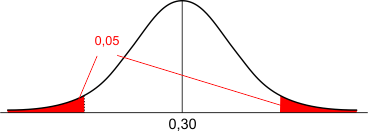
Echter, jouw gevonden p-waarde (let op: de p in p-waarde is niet de p van proportie!) 0,0809 is groter dan 0,05. Deze p=waarde geeft de groen gearceerde oppervakte weer, zie de figuur hieronder.
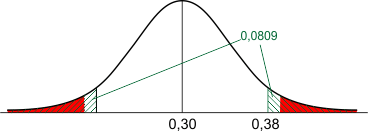
Dit betekent dat de gevonden proportie 0,38 niet ver genoeg verwijderd is van de verwachte waarde 0,30 om te veronderstellen dat de nulhypothese onwaar is. Er is geen aanleiding om H0 te verwerpen, er is onvoldoende bewijs dat doofheid te maken heeft met de kleur ogen.
Dan vraag b. Nu is de bewering dat katten met blauwe ogen vaker doof zijn dan andere katten. H0 blijft de aanname dat er geen invloed is, maar de alternatieve hypothese anders: deze is niet langer dat er een willekeurige invloed is (vaker doof of minder vaak doof), maar dat katten met blauwe ogen vaker doof zijn. Dus:
H0: p=0,30
H1: p$>$0,30
In plaats van een tweezijdige toets (zoals bij vraag a) moeten we nu een eenzijdig toets uitvoeren: de nulhypothese kan alleen worden verworpen wanneer de gevonden proportie in voldoende mate groter is dan 0,30. In dat geval ligt het rode gebied met oppervlakte 0,05 geheel aan de rechter kant (in plaats van verdeeld over 2x 0,025 zoals bij vraag a):
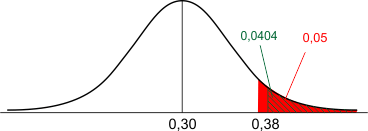
De p-waarde is nu maar 0,0404. Immers, het gearceerde oppervlak links is vervallen, want wanneer de steekproefproportie in dit gebied zou vallen, dan zouden we nog steeds bij de nulhypothese blijven.
Omdat nu geldt: p-waarde$<$0,05 (dus: gevonden proportie in het rode gebied) verwerpen we de nulhypothese en accepteren we de alternatieve hypothese: we nemen aan dat katten met blauwe ogen vaker doof zijn dan andere katten.
Je ziet: bij dit soort toetsen moet je de onderzoeksvraag nauwkeurig formuleren. Bij een iets andere onderzoeksvraag kom je op grond van dezelfde gegevens tot een andere conclusie.

|
Vragen naar aanleiding van dit antwoord? Klik rechts..!
woensdag 10 juni 2020
|

|



home |
vandaag |
bijzonder |
gastenboek |
statistieken |
wie is wie? |
verhalen |
colofon
©2001-2024 WisFaq - versie 3
|












