WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Examen vraag mbo 81-82

Ik wil nog effe de puntjes op de i zetten bij de volgende opgave. Het meeste heb ik goed.

Ten opzichte van een rechthoekig assenstelsel OXYZ zijn A(3,3,0), B(-3,3,0), C(-3,-3,0), D(3,-3,0) en T(0,0,9). Punt M is het midden van CT.
Teken de piramide T·ABCD.
Geef een vectorvoorstelling van het vlak door A, B en M.
Bereken de afstand van punt D tot vlak V.
Geef een vectorvoorstelling van de lijn door D die evenwijdig is aan het vlak V en aan het vlak door B, C en T.
Bij a. heb ik gewoon een schatting gemaakt van de punten om de piramide te tekenen. Heb je hier een werkwijze voor? Met name voor de x-as. Ik neem ik 2 naar rechts 1 omhoog.

Bij b. heb ik van deze examen vraag voor het vlak V (3,3,0)+l(-6,0,0)+m(-1,-1,1)
Het model heeft hier : (3,3,0)+l(1,0,0)+m(1,1,-1)
Ik neem aan dat dit precies hetzelfde is?

Bij c. heb ik het antwoord goed maar hoop niet dat dat toevallig is.

Bij d. loop ik vast.

Ik heb mijn uitwerking opgestuurd.
mboudd
Leerling mbo - zaterdag 18 april 2020

Antwoord

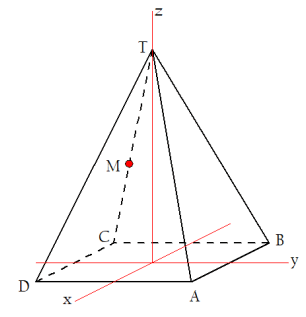Je tekening is aardig goed, maar meestal teken je afstanden op de schuine as (de x-as) ongeveer de helft van echte afstanden. Dat krijg je bovenstaande tekening.
Dat is hetzelfde. Het is meestal wel handig om de richtingsvectoren zo eenvoudig mogelijk te nemen. Dat scheelt rekenwerk.
Dat zal geen toeval zijn...
Bepaal de snijlijn van V en het vlak BCT. De lijn door D evenwijdig aan V en BCT is evenwijdig aan de snijlijn.
Dat moet lukken!

Vragen naar aanleiding van dit antwoord? Klik rechts..!
zaterdag 18 april 2020

Re: Examenopgave mbo 82-83