WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

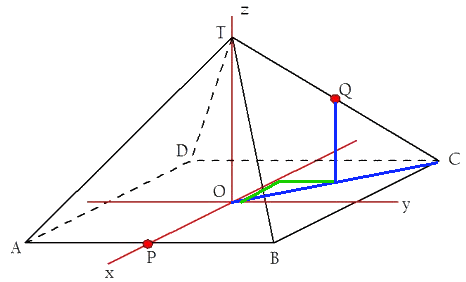
Re: Re: Re: Re: Regelmatige 4-zijdige piramide

Dit is een reactie op vraag 89496

Ja, bij ABCD heb je geen steunvector omdat deze al in O ligt? Daar komt uit l(0,1,0)+m(1,0,0). Volgens het model (begrijpelijk).

Bij b. kom ik voor de lijn PQ op:

(3,0,0)+l(Q-P)=(3,0,0)+l(-6,0,3).

De PQ van het model geeft echter (3,0,0)+l(9,-3,-4)
Hoe komen ze hier aan?
mboudd
Leerling mbo - woensdag 1 april 2020

Antwoord

Het idee is goed maar ik denk dat je de coördinaten van $Q$ niet goed hebt.

$
P(3,0,0)
$
$
Q\left( { - 1\frac{1}{2},1\frac{1}{2},2} \right)
$
$
PQ = \left( { 4\frac{1}{2},-1\frac{1}{2},-2} \right) \equiv \left( {9, - 3, - 4} \right)
$.

Teken driehoek $OCT$ maar 's.

Helpt dat?

Vragen naar aanleiding van dit antwoord? Klik rechts..!
woensdag 1 april 2020

Re: Re: Re: Re: Re: Regelmatige 4-zijdige piramide