WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Re: Re: Re: Constructie van een cirkel die twee gegeven cirkels snijdt

Dit is een reactie op vraag 89375

Hartelijk dank voor de informatie,
Toch zonder jouw hulp kan ik echt niet verder. Wil je aub even zien of ik het goed gedaan, want tot heden lukt mij niet de cirkel door P moet te tekenen. Ik zit eerlijk gezegd nog vast. Waar loop ik verkeerd eigenlijk? Alvast bedankt
M
Student hbo - zaterdag 21 maart 2020

Antwoord

Beste M,

Ik heb een figuur voor je gemaakt.

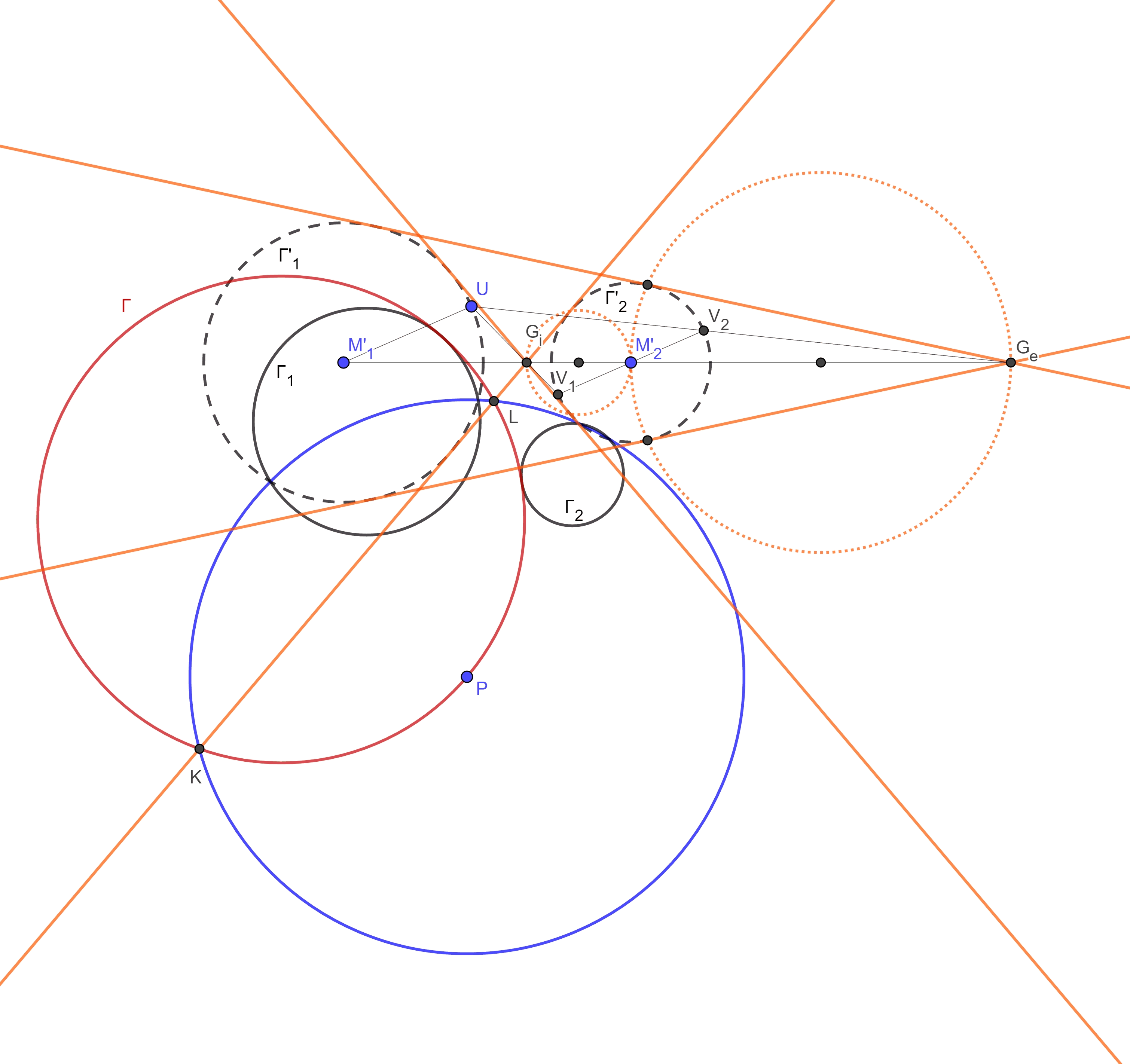
We hebben punt $P$ en cirkels $\Gamma_1$ en $\Gamma_2$. We kiezen een inversiecirkel met middelpunt $P$ (blauw).

De inverses van $\Gamma_1$ en $\Gamma_2$ zijn $\Gamma'_1$ en $\Gamma'_2$ (gestreept) met middelpunten $M'_1$ en $M'_2$.

Nu de raaklijnen:
Op $\Gamma_1$ kies ik een punt $U$. Dan construeer ik diameter $V_1V_2$ van $\Gamma_2$ zodat $V_1V_2$ evenwijdig is met $M'_1U$.
Vervolgens snijd ik $UV_1$ met $M'_1M'_2$ om het interne gelijkvormigheidspunt $G_i$ te vinden. Met $UV_2$ vind ik net zo het externe gelijkvormigheidspunt $G_e$ (al deze lijntjes zijn dun).

Nu teken ik de cirkels met diameter $G_iM'_2$ en $G_eM'_2$ (oranje gestippeld) (Dit had ook met $M'_1$ gemogen, maar dat komt in dit plaatje minder goed uit).

Deze snijden $\Gamma'_2$. Ik verbind $G_i$ en $G_e$ met de bijbehorende snijpunten en daarmee heb ik de (oranje) raaklijnen te pakken. Je ziet dat deze raaklijnen beide cirkels $\Gamma'_1$ en $\Gamma'_2$ raken.

Ik heb er een raaklijn uitgepikt en de snijpunten $K$ en $L$ met de inversiecirkel bepaald. De cirkel door $K$, $L$ en $P$ is nu de inverse van die raaklijn. En zoals je ziet raakt die de gegeven cirkels $\Gamma_1$ en $\Gamma_2$.

Zo kan dat ook met de andere raaklijnen. Bij de raaklijn die niet de inversiecirkel snijdt kan je het iets anders doen.

De raakpunten $R$ en $S$ van deze raaklijn met $\Gamma'_1$ en $\Gamma'_2$ kun je makkelijk inverteren. De inverse van $R$ is bijvoorbeeld het snijpunt van $RP$ met $\Gamma_1$ dat binnen de inversiecirkel ligt. Nu is de cirkel door $R'$, $S'$ en $P$ een raakcirkel van $\Gamma_1$ en $\Gamma_2$.

Met vriendelijke groet,

Vragen naar aanleiding van dit antwoord? Klik rechts..!
zaterdag 21 maart 2020