WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Re: Maximale oppervlakte van driehoek

Dit is een reactie op vraag 89192

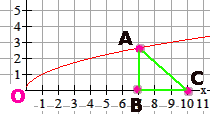
Ik snap de projectie, maar hoe druk je de oppervlakte uit in x. Kom je geen gegevens te kort?
chanta
Leerling bovenbouw havo-vwo - maandag 2 maart 2020

Antwoord

Neem de $x$-coördinaat van B als je variabele. De lengte van BC is dan gelijk aan $10-x$ en de lengte van AB is gelijk aan $f(x)$. Dat ben je al een eind op weg.

De oppervlakte van de driehoek is gelijk aan een half maal zijde maal hoogte. In de tekening is de zijde gelijk aan $10-x$. De hoogte is $f(x)$, dus de formule voor de oppervlakte van de driehoek uitgedrukt in $x$ is:

$
\eqalign{O(x) = \frac{1}
{2}\left( {10 - x} \right) \cdot \sqrt x }
$

Dan moet het wel lukken?

PS
Jij schreef C(12,0) maar ik heb hier C(10,0) genomen. Dat maakt voor het 'idee' niet veel uit maar 't scheelt mij weer een tekening. Ik blijf niet aan de gang...

Vragen naar aanleiding van dit antwoord? Klik rechts..!
maandag 2 maart 2020