WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Vergelijkingen bij meetkundige figuren

Dit is de opdracht:

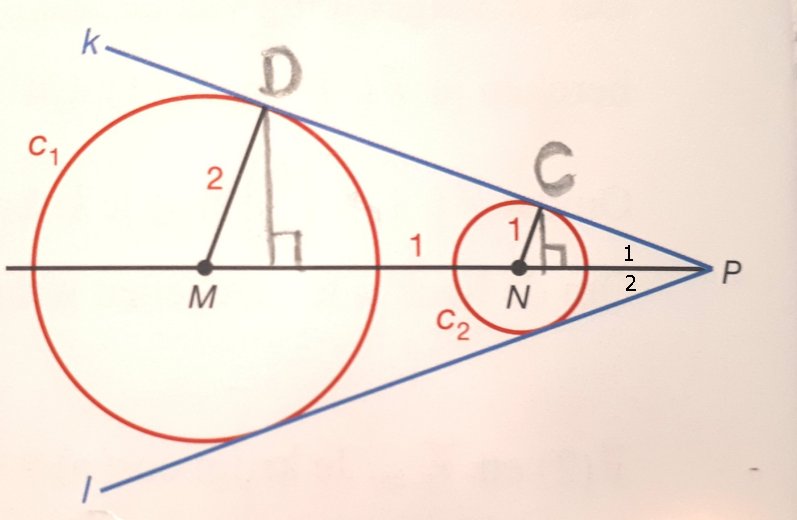
Gegeven zijn de cirkel c1 met middelpunt M en straal 2 en cirkel c2 met middelpunt N en straal 1. De afstand tussen beide cirkels is 1. De gemeenschappelijke raaklijnen k en l snijden elkaar in het punt P. Zie het figuur wat ik stuur via de mail voor de plaatjes.
Bereken exact sin(hoek(k,l))
Ik heb al NP gelijkgesteld aan x. Daarna heb ik vastgesteld dat driehoek MPD gelijk is aan driehoek NPC. Dit geeft:

MP/NP = MD/NC
(4 + x)/x = 2/1
2x = 4 + x
x = 4
dus NP = 4

Ik weet alleen niet meer wat ik hierna moet doen. Zouden jullie mij kunnen helpen. Alvast bedankt!
Sven
Leerling bovenbouw havo-vwo - vrijdag 17 januari 2020

Antwoord

Je weet nu:

$
\eqalign{
& \sin \angle P_1 = \frac{1}
{4} \cr
& \cos \angle P_1 = \frac{\sqrt {15}}
{4} \cr
& \angle P_1 = \angle P_2 \cr}
$

De vraag is dan wat $
\sin \angle P
$ dan is...

In 't algemeen geldt:

$
\sin (2A) = 2\sin (A)\cos (A)
$

...en dan ben je er wel... Lukt dat?

Vragen naar aanleiding van dit antwoord? Klik rechts..!
vrijdag 17 januari 2020