|
|
|
\require{AMSmath}



Standaardafwijking berekenen bij een normaalverdeling
Een bakker bakt broden van 1000 gram. Normaal verdeeld. Wat is de standaardafwijkingen als het gemiddelde gewicht 1000 gram is en 5% van de broden minder weegt dan 900 gram? Ik heb een gr TI-84 Plus. Ik vul eerst bij Y1 in: normcdf (-10^99, 900, 1000, X). Bij Y2 0,05. Dan ga ik naar window en vul bij X min = 0, en bij Ymin ook 0 in. Wat vul ik bij Xmax en Ymax in? Welke knoppen moet ik nu verder indrukken?
Saskia
Student hbo - vrijdag 19 januari 2018
Antwoord
Hallo Saskia,
Voor het instellen van het window maak je een ruwe schatting van de x- en y-waarden van het snijpunt van Y1 en Y2. Immers, je wilt dit snijpunt straks binnen het window zien.
In de Y-richting is dit niet zo moeilijk: Y2 is constant, 0,05. Het snijpunt komt dus hoe dan ook op hoogte Y=0,05 te liggen. Wanneer je kiest: YMIN=0 en YMAX=0,10, dan ligt het snijpunt straks mooi in het midden van de hoogte van je scherm. Je kunt ook YMAX=0,15 of YMAX=0,20 kiezen. Dan zie je een groter deel van de functie Y1, dat kan handig zijn wanneer je het snijpunt niet zo goed geschat hebt. Maar kies niet YMAX=20 of YMAX=100! Als je dat zou doen, dan worden de grafieken van Y1 en Y2 platgedrukt tegen de onderkant van je scherm.
Kortom: maak een redelijke schatting, kies liever een iets te ruim window dan iets te krap, maar niet 10x of 100x te ruim.
Voor de X-as moet je bedenken wat X voorstelt: in dit geval is X de (gezochte) standaardafwijking. Een standaardafwijking is nooit negatief, dus XMIN=0 is prima.
Voor XMAX maken we weer een schatting hoe groot deze standaardafwijking ongeveer zou kunnen zijn. Eerst maar even een schets (zoals je natuurlijk bij elke vraag over de normaalverdeling maakt):
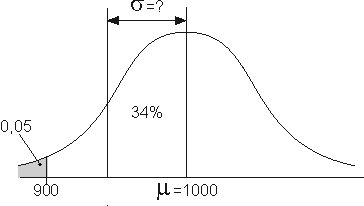
Wanneer je vanuit het gemiddelde 1 keer de standaardafwijking naar links gaat, dan is volgens de vuistregels van de normaalverdeling de oppervlakte onder dit deel van de curve 34% van de totale oppervlakte. Verder naar links is dan nog 50-34=16% over. Volgens de gegevens is de oppervlakte links van 900 gram 5%. De standaardafwijking is dus ruim kleiner dan 1000-900, dus ruim kleiner dan 100. Kies XMAX=100, dan weet je zeker dat de werkelijke waarde straks binnen het window valt.
Samengevat
Maak een ruwe schatting van de waarde die je gaat vinden (hier: met behulp van de vuistregels voor de normaalverdeling). Kies je window gerust 2x, 5x of eventueel 10x wijder dan je schatting. Hiermee voorkom je dat grafieken bij een iets verkeerde schatting buiten het window komen, dan zie je gelijk niets meer. Maar kies niet 100x of 1000x te wijd, want dan verschrompelen je curven tot platte figuren (rechte lijnen).
OK zo?

|
Vragen naar aanleiding van dit antwoord? Klik rechts..!
vrijdag 19 januari 2018
|

|



home |
vandaag |
bijzonder |
gastenboek |
statistieken |
wie is wie? |
verhalen |
colofon
©2001-2024 WisFaq - versie 3
|











 Re: Normale verdeling
Re: Normale verdeling