WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Horizontale asymptoot van een vierkantswortel

Hallo,
Mijn opgave is $y=\sqrt{(x+1)(x-3)}$.
Deze opgave heeft geen verticale asymptoot, maar hoe bereken je van een functie onder een wortel de horizontale asymptoot?

Groetjes
Xavier
Student Hoger Onderwijs België - zaterdag 6 januari 2018

Antwoord

Hallo Xavier,

Deze kromme heeft ook geen horizontale asymptoot. Daar lijkt het ook helemaal niet op als je een schets gaat maken van de grafiek.
Je ziet dan dat de grafiek naar links en rechts algauw bijna als een rechte lijn omhoog loopt, naar oneindig.

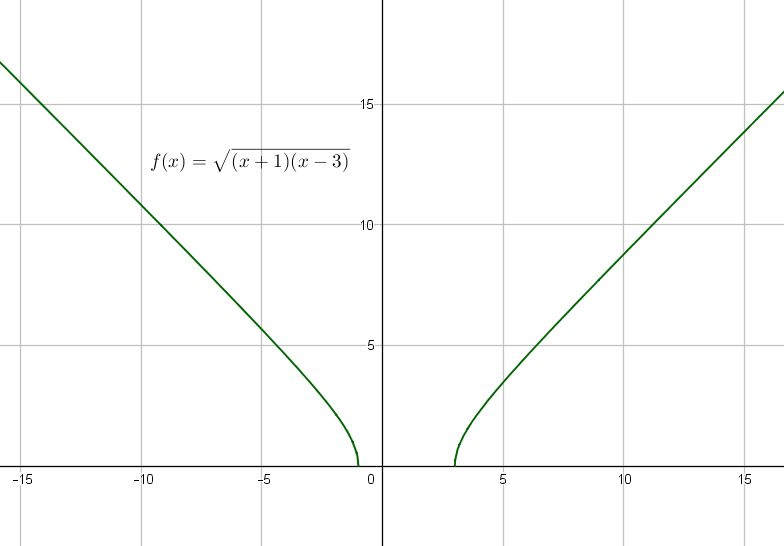
Dat zou suggereren dat er misschien links en rechts een scheve asymptoot loopt.

We kunnen dat aantonen door het kwadraat af te splitsen van hetgeen er onder het wortelteken staat: $(x+1)(x-3)=x^2-2x-3=(x-1)^2-4$.

De kromme is dus gelijk aan $y=\sqrt{(x-1)^2-4}$. Nu is duidelijk dat als $x$ naar $\pm\infty$ gaat, dat deze kromme dan nadert naar $y=\sqrt{(x-1)^2}=|x-1|$.

Dus er zijn inderdaad twee scheve asymptoten, $y=x-1$ en $y=-x+1$.

Groeten,

Vragen naar aanleiding van dit antwoord? Klik rechts..!
zaterdag 6 januari 2018