WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Extremumprobleem en afgeleide

Hallo,

We moeten een vraagstuk oplossen, maar ik weet niet hoe te beginnen.

Een muur van 2 meter hoog bevindt zich op 1 meter van een gebouw. Bepaal de lengte van de kortste ladder die steunt op de grond en leunt tegen de muur en tegen het gebouw.

We moeten een goniometrische vergelijking uitkomen en hier de afgeleide van berekenen. Ik weet dat we een minimum moeten zoeken maar voor de rest kan ik er niet aan uit..

Alvast bedankt!
Chris
3de graad ASO - zondag 29 september 2013

Antwoord

Hoi,

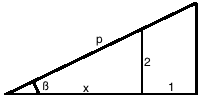
Op de afbeelding zie je met welke situatie we te maken hebben, en heb ik voor de makkelijkheid ook wat dingen een naam gegeven: de hoek ß die de ladder maakt met de grond, de schuine zijde p (tot tegen de muur), en de horizontale afstand x tussen de muur en de plek waar de ladder op de grond staat.

Nu moet je proberen in functie van ß te berekenen wat p is. Dit kan je doen door eerst x te berekenen: x = 2/tanß, en daarna kan je p berekenen: p = (x+1)/cosß. Als je dit dan nog wat verder uitwerkt krijg je dus dat p een functie is in functie van ß. Je kan schrijven dat p = 2/sin(ß) + 1/cos(ß).

Nu wil je dat p zo klein mogelijk is (een minimum dus inderdaad), en dat doe je door de afgeleide van p (in functie van ß) te berekenen, en van die afgeleide de nulpunt(en) te berekenen (op het interval ]0,pi/2[ logischerwijs).

Een andere beantwoorder wist op te merken dat er een veel eenvoudigere oplossing is, maar deze werkt zonder goniometrische vergelijking: je hebt enkel de stelling van Pythagoras en wat basiskennis van gelijkvormige driehoeken nodig:

(stel dat y de hoogte is waar de ladder tegen het gebouw leunt)

$p^2=(x+1)^2+y^2$
met $\eqalign{\frac{2}{x}=\frac{y}{x+1} \Rightarrow y=\frac{2x+2}{x}}$
geeft:
$\eqalign{p^2=\frac{(x+1)^2(x^2+4)}{x^2}}$

Zoeken naar het maximum voor $p^2$ geeft:

$\eqalign{\frac{2(x+1)(x^3-4)}{x^3}}$
$\eqalign{\frac{2(x+1)(x^3-4)}{x^3}=0}$ geeft dat $p^2$ is maximaal voor $\eqalign{x=\sqrt[3]{4}}$

Mvg

Vragen naar aanleiding van dit antwoord? Klik rechts..!
zondag 29 september 2013