WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Horizontale raaklijnen

Ik probeer wat wijzer te worden nu zit ik met de volgende opgave:

Voor wat voor waardes van x heeft de tekening f(x) = 2x³-4x²-9x+100 een hoizontale raaklijn.

Zou u dit voor mij uit kunnen leggen hoe ik dit bereken?

Andre
Ouder - maandag 14 juli 2003

Antwoord

Een horizontale raaklijn treedt op in de punten x waar de afgeleide van de functie nul is. Een aantal notaties voor afgeleide: f'(x)=(D(f))(x)=0 oplossen naar x.

Je ziet dat de functie f(x) een veeltermfunctie is van de derde graad.

1)Je moet ook weten dat de afgeleide van een som gelijk is aan de som van de afgeleiden.
of anders: D(f(x)+g(x))=D(f(x)) + D(g(x))

2)En de afgeleide van een functie vermenigvuldigd met een constant getal is gelijk aan de afgeleide van de functie vermenigvuldigd met dat getal.
of anders: D(c·f(x)) = c·D(f(x))

Dus D(2x³-4x²-9x+100)
Na toepassing van 1)
= D(2x³) + D(-4x²) + D(-9x) +D(100)
Na toepassing van 2)
=2·D(x³) -4·D(x²) -9·D(x) + 0
van de afgeleide van een constant getal is 0 dus D(100)=0

Nu is de afgeleide van een macht van x gelijk aan x tot die macht-1 vermenigvuldigd met de oorspronkelijke macht.
of anders D(xⁿ) = n·x^(n-1)

Dus
=2·3·x² - 4·2·x¹ - 9·1·x⁰
=6x²-8x-9

Dit is de afgeleide van de functie f(x)

Om de x-waarden waar er een horizontale raaklijn is te kennen moet je dit nul stellen en oplossen naar x.
Dus 6x²-8x-9=0
Met abc-formule:

x₁=(8+Ö(64+4·6·9))/12=2/3+1/6·Ö70
x₂=(8-Ö(64+4·6·9))/12=2/3-1/6·Ö70

Hier een figuur:

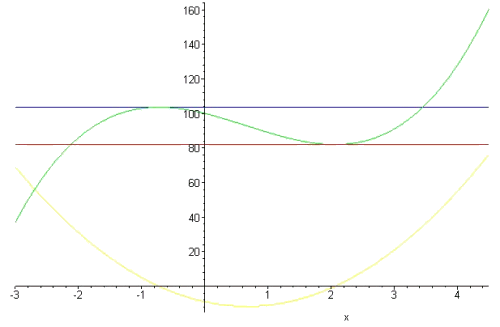
De groene kromme is f(x), de gele is de afgeleide f'(x) en de rode en de blauwe zijn de raaklijnen.

Vragen naar aanleiding van dit antwoord? Klik rechts..!
maandag 14 juli 2003