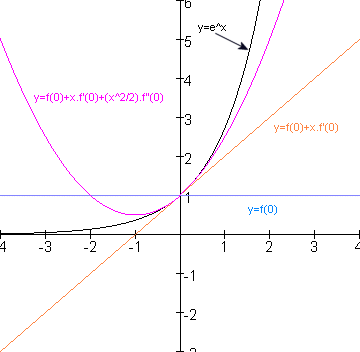WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Taylor polynomen

Hi,

Kan iemand mij uitleggen waarom het blijkbaar correct is om bij een Taylor polynoom die je niet in het centrum uitrekent, maar in een willekeurige waarde c, (x-c) in te vullen op iedere x positie en c in te vullen op iedere 0 positie? (zoals in verschillende uitleggen als ´logische´ stap wordt gepresenteerd)
Ik snap dit niet omdat als je een afgeleide toepast op 0 je eigenlijk alleen de constante in die afgeleide overhoud, maar als je een c != 0 gebruikt gaat die vlieger niet op. Dus aan de ene kant heb je die x-c factor die dicht bij nul ligt (net zoals in de originele situatie) en aan de andere kant heb je een c die misschien wel helemaal niet dicht bij nul ligt, maar ze worden wel alletwee gesubstitueerd in dezelfde formule.....ik niet begrijp, help!
Sieme
Student Hoger Onderwijs België - maandag 9 juni 2003

Antwoord

Eerst even over het begrip van een Taylorpolynoom. Wat doet dat?
Stel je hebt een of andere willekeurige functie f(x) en die wil je gaan benaderen door c,x,x²,x³ etc...
en wel rond het punt x=0.

1. de meest ruwe schatting van het gedrag van f(x) rond x=0 is natuurlijk f(0). Dus de lijn y=f(0) benadert f(x) vlakbij x=0 redelijk, maar al heel gauw loopt f(x) weg van y=f(0)
2. een iets betere (maar nog steeds zeer ruwe) benadering van f(x) rond x=0 zou zijn een schuine lijn die gelijk oploopt met f(x) in x=0.
Dit is een lijn met as-afsnede f(0) en richtingscoefficient f'(0):
y=f(0)+x.f'(0)
3. Dit laatste gaat in de buurt van x=0 goed, maar als f(x) gekromd is, kan die 'starre' richtingscoefficient (bij punt 2) deze kromming niet bijhouden.
Een nog ietsje betere benadering zou dus zijn om in de benaderingscurve iets van de kromming mee te pakken:
y=f(0)+x.f'(0)+(x²/2).f'(0)

etc...
hieronder heb ik dit geillustreerd a.h.v. f(x)=e^x

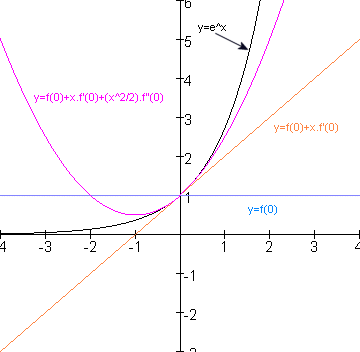
Verder:
Je weet waarschijnlijk dat wanneer je in een bepaalde functie g(x) alle x'en vervangt door (x-a), dat daarmee de grafiek van de functie over een afstand a naar rechts getransleerd wordt. (probeer maar eens met -bijv-
y=sinx+√x (teken dit) en teken daarna eens de curve y=sin(x-2)+√(x-2). Je zult zien dat de 2e curve ontstaat uit de 1e curve welke getransleerd is over 2 naar rechts)

Nu weer terug naar jouw probleem:
Hoe zit dat met Taylorbenaderingen rond x=c ipv rond x=0.
We doen het volgende:
Ten eerste transleren we in gedachten onze functie f(x) over een afstand c naar links (aangenomen dat c$>$0). Zodoende gaat f(x) over in f(x+c);
Ten tweede gaan we een Taylorbenadering maken rond x=0
Ten derde gaan we deze Taylorbenadering weer terugtransleren over c naar rechts.

een Taylorbenadering van f(x+c) rond x=0 ziet er als volgt uit:
f(x+c)=f(0+c)+x.f'(0+c)+(x²/2).f'(0+c)+...
=f(c)+x.f'(c)+(x²/2).f'(c)+...

Nu gaan we deze Taylorbenadering in zijn geheel weer terugtransleren over afstand c naar rechts.
Hierbij gaat in de Taylorreeks elke x over in x-c.
Dit levert
f(c)+(x-c).f'(c)+((x-c)²/2).f'(c)+...+((x-c)ⁿ/n!).fⁿ(c)

groeten,
martijn

Vragen naar aanleiding van dit antwoord? Klik rechts..!
maandag 9 juni 2003