|
|
|
\require{AMSmath}



Bewijzen voor de stelling van Pythagoras
Wij moeten voor wiskunde een praktische opdracht maken over Pythagoras. Wij willen graag 5 bewijzen hebben voor de stelling van Pythagoras. Het liefst in het Nederlands.
Anita
Leerling bovenbouw havo-vwo - donderdag 6 februari 2003
Antwoord

Beste Anita,
Ik heb wel een site kunnen vinden in het Engels, die is gegeven helemaal hieronder. Daarop kun je 122 bewijzen vinden. Hieronder heb ik er 5 geselecteerd, waar je zelf nog wel het bewijs van moet maken, maar dat moet wel lukken met de aanwijzingen.
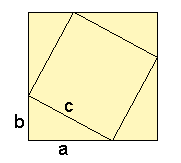
Bewijs 1: vierkant met zijde a+b
Het volgende vierkant heeft zijden a+b.
Wat is dan de oppervlakte?
Het vierkant kan worden verdeeld in 4 driehoeken en een vierkant. Wat zijn de formaten van deze driehoeken en het vierkant?
Stel deze twee gegevens aan elkaar gelijk en dan vind je na wat uitwerken de stelling van Pythagoras
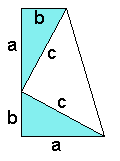
Bewijs 2: trapezium
Dit bewijs lijkt wel wat op het vorige bewijs.
Bereken de oppervlakte van het trapezium door de afzonderlijke stukjes op te tellen en door met de buitenafmetingen van het trapezium de oppervlakte uit te rekenen. (Hoogte maal het gemiddelde van de bovenzijde en onderzijde)
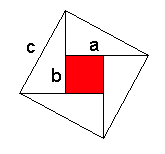
Bewijs 3: vierkant met zijden c
Pas in een vierkant met zijden c, vier pythagoras driehoeken. Er blijft dan in het midden een vierkant over.
De oppervlakte van het vierkant kan weer op twee manieren worden berekend: als c2 en als som van de vier driehoeken en het kleine vierkant.
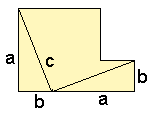
Bewijs 4: Twee vierkanten
Teken twee vierkanten naast elkaar: met zijde a en zijde b.
Trek twee lijnen in dit figuur. De twee driehoeken die ontstaan kun je zo verplaatsen dat je een vierkant met zijde c krijgt.
Bewijs 5: Gelijke oppervlakte
Teken op de rechthoekige driehoek op de zijde vierkanten. Verdeel het vierkant op de schuine zijde in twee stukken door een hoogtelijn vanuit de punt door te trekken.
Begin met de eerste deel van dat vierkant. Dat kun je verschuiven naar een parallelogram van dezelfde oppervlakte. Bewijs waarom de oppervlakte hetzelfde is. Draai dan dit parallogram. Bewijs dat het precies zoals op de tekening uitkomt. Dan kun je weer bewijzen dat dit parallelogram gelijk is aan een van de andere vierkanten. Dan kun je hetzelfde doen met het andere deel van het grote vierkant.
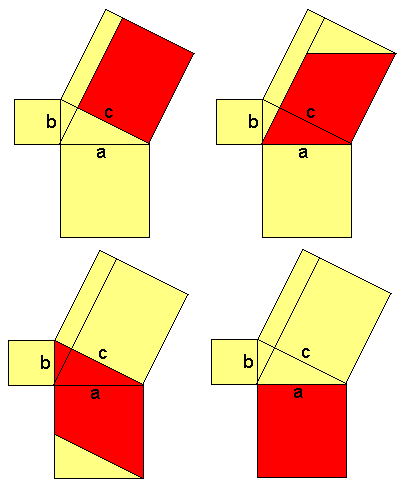
Je moet nu nog wel wat zelf bewijzen. Maar ik hoop dat dit stuk je voldoende aanwijzingen geeft. Er zijn op internet nog wel wat andere bewijzen te vinden. Die zul je ook wel begrijpen, omdat de figuren erbij vaak al heel veel informatie geven. Heel veel succes, het zal veel voldoening geven zelf het bewijs te maken, en kom je er nog niet helemaal uit, dan kun je hier natuurlijk weer een vraag stellen.
Zie 122 bewijzen voor de stelling van Pythagoras

|
Vragen naar aanleiding van dit antwoord? Klik rechts..!
maandag 10 februari 2003
|

|



home |
vandaag |
bijzonder |
gastenboek |
statistieken |
wie is wie? |
verhalen |
colofon
©2001-2024 WisFaq - versie 3
|















