 |
De digitale vraagbaak voor het wiskundeonderwijshome | vandaag | gisteren | bijzonder | gastenboek | wie is wie? | verhalen | contact |
|||||||||||||||||||
|
\require{AMSmath}



Ongelijkzijdige afgeronde driehoek
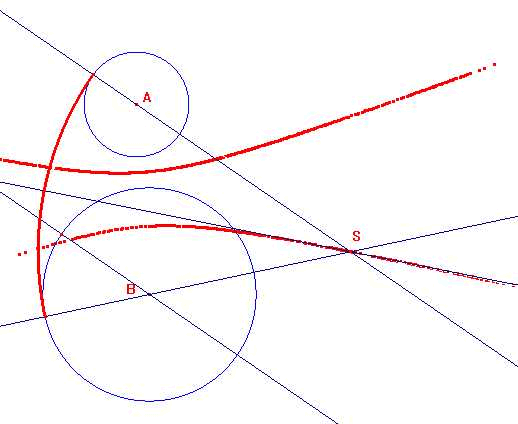
AntwoordAls je de boogvan A en B wilt tekenen dan teken je een lijn door het punt waar de cirkel overgaat in de boog en het middelpunt A van de cirkel. Idemdito voor de cirkel met middelpunt B. Daar waar de lijnen elkaar snijden ligt het middelpunt S van de boog.



home | vandaag | bijzonder | gastenboek | statistieken | wie is wie? | verhalen | colofon ©2001-2024 WisFaq - versie 3
| |||||||||||||||||||





 Re: Ongelijkzijdige afgeronde driehoek
Re: Ongelijkzijdige afgeronde driehoek