|
|
|
\require{AMSmath}



Rechthoekige driehoek
Een plaatje in de vorm van een rechthoekige driehoek
ABC heeft een rechte hoek bij C en rechthoekszijden
AC=12cm en BC=8cm. Het plaatje wordt in twee rechthoekige driehoeken ADC en DBC gezaagd.- Bereken de lengtes van de rechthoekszijden van die twee rechthoekige driehoeken in mm nauwkeurig en bereken de hoeken ervan.
Hoe precies gaat deze 'totale' driehoek er uit zien?
Thomas
Student hbo - woensdag 7 oktober 2020
Antwoord
Hallo Thomas,
Om met jouw laatste vraag te beginnen: je driehoek ziet er zo uit:
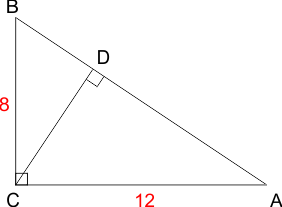
De zijde AB kan je berekenen met de stelling van Pythagoras.
Om de zijden van de kleine driehoeken te berekenen, toon je eerst aan dat de driehoeken ABC, ACD en CBD gelijkvormig zijn. Lukt dit?
Wanneer je deze gelijkvormigheid hebt aangetoond, dan geldt kennelijk:
AB:BC:AC = AC:CD:AD = CB:CD:BD
Met deze verhoudingen kan je de lengte van alle lijnstukken in de figuur berekenen.
Hoeken bereken je met goniometrie. Voor hoek A geldt bijvoorbeeld:
tan(hoek A) = BC/AC = 8/12
Hoek A = tan-1(8/12)
Hoek B bereken je op soortgelijke wijze, of je maakt gebruik van de stelling dat de drie hoeken van een driehoek samen altijd 180° zijn.
Hiermee zijn alle hoeken bekend, want de drie driehoeken hebben gelijke hoeken (ze zijn immers gelijkvormig).

|
Vragen naar aanleiding van dit antwoord? Klik rechts..!
donderdag 8 oktober 2020
|

|



home |
vandaag |
bijzonder |
gastenboek |
statistieken |
wie is wie? |
verhalen |
colofon
©2001-2024 WisFaq - versie 3
|










