|
|
|
\require{AMSmath}



Re: Onleesbaar rijksregisternummer berekenen
Dat lukt me dus niet, tenzij ik gewoon elk getal invul en het controlegetal controleer. Maar echt wiskundig kun je dat niet noemen.
Als ik dan het omgekeerde probeer, dus vertrek vanuit mijn controlegetal, raak ik niet verder dan het feit dat de rest van de deling 97-61=36 moet zijn. Daarna loop ik vast, omdat je toch niet weet bij welk getal je die 36 dan moet optellen (het 'begingetal' gedeeld door 97 is 'iets' + 36)?
Zou je dit voorbeeld dan eens kunnen uitwerken zodat ik het wel begrijp?
Dank je!
Janne
3de graad ASO - zaterdag 22 maart 2014
Antwoord
Het ging om 930?1822361. Wat staat er op het vraagteken?
Je zoekt een cijfer $n$ zodat MOD(930018223+$n$·100000,97)=36. Er zijn voor $n$ slechts 10 mogelijkheden. Wat is er mis mee om die even uit te proberen? Als je een oplossing vindt dan weet je ook zeker dat het goed is.
Ik heb ik Excel even een lijstje gemaakt met de 10 mogelijkheden en 't blijkt dat $n$=5 de oplossing is.
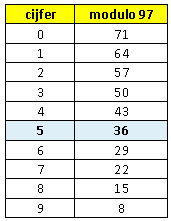
In de rechter kolom staat '=modulo(930018223+B2·100000;97)'. Ik moest wel even een functie maken:Function modulo(a, m)
modulo = a - Int(a / m) · m
End Function Dat werkt.
Berekening
Als je 't wil berekenen dan kan dat ook:
930018223+n·100000 mod 97 = 36
mod(930018223,97)=71
n·100000 mod 97 = 62
mod(100000,97)=90
de inverse van 90 (mod 97) is 83
62 x 83 = 5 (mod 97)
n=5
Moet kunnen...

|
Vragen naar aanleiding van dit antwoord? Klik rechts..!
zaterdag 22 maart 2014
|

|



home |
vandaag |
bijzonder |
gastenboek |
statistieken |
wie is wie? |
verhalen |
colofon
©2001-2024 WisFaq - versie 3
|








 Dit is een reactie op vraag 72566
Dit is een reactie op vraag 72566 


