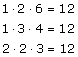WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Drie opgaven over kansberekening

We hebben 50 opgaven over kansberekening gekregen, een aantal vragen kom ik niet, dit zijn de volgenden:

Vraag 1
Leeftijd:           15   16   17   18
aantal leerlingen:  17   42   16    4
Er wordt een vertegenwoordiging van vijf leerlingen gekozen.
Bereken de kans op een vertegenwoordiging
a. met precies drie 16-jarigen.
b. met leerlingen die allemaal dezelfde leeftijd hebben.

Vraag 2
Kees gooit met drie gewone dobbelstenen.
Bereken exact! de kans dat
a. het product van de drie ogenaantallen gelijk is aan 12.
b. het product even is.

Vraag 3
Bij een loterij zijn 200 loten verkocht voor 3 euro per stuk. Er zijn twee prijzen van elk 50 euro en tien prijzen van elk 20 euro. Op elk lot kan niet meer dan 1 prijs vallen.
Leonie heeft 6 loten gekocht.
Bereken de kans dat Leonie
a. minder dan twee prijzen wint.
b. precies 100 wint.
c. geen verlies lijdt bij deze loterij.

Serena
Leerling bovenbouw havo-vwo - maandag 11 mei 2009

Antwoord

Ik zie verder geen enkele aanwijzing over je eigen oplossing of pogingen daartoe zodat ik je een aantal hints zal geven. Misschien heb je er iets aan. Misschien kan je ook de spelregels eens lezen?

Vraag 1
Dit kan handig met de 5. Hypergeometrische verdeling.

Vraag 2
a.
Schrijf eerst eens alle combinaties op van drie dobbelstenen die vermendigvuldigd 12 geven:

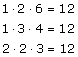
Elke combinatie kan natuurlijk op verschillende volgordes tot stand komen:

In totaal zijn er 15 (heb ik ze allemaal gehad?) verschillende volgordes van dobbelstenen die vermenigvuldigt 12 geven. In totaal zijn er 6³ verschillende volgordes die allemaal dezelfde kans hebben. Dus de kans op 'product is 12' is gelijk aan....

b.
Op dezelfde manier als a.

Opgave 3
Toen had ik geen zin meer... maar gestructureerd alle mogelijkheden opschrijven zou hierbij moeten werken. Verder is het dan zonder terugleggen...

Vragen naar aanleiding van dit antwoord? Klik rechts..!
donderdag 14 mei 2009