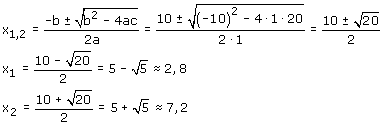|
|
|
\require{AMSmath}



ABC formule
Zou u -2x≤+20x=40 op kunnen lossen door middel van de ABC formule ook graag uitleg waarom je het zo doet. Ik zou het heel erg op prijs stellen als u de hele som laat zien.
Op school moeten we nou inklemmen en als ik vraag naar de ABC formule wilt hij het niet geven. Dus vandaar dat ik het aan u vraag...
Jordy
Leerling bovenbouw vmbo - woensdag 23 februari 2005
Antwoord
Als je een tweedegraads vergelijking wilt oplossen met de ABC-formule dan moet je eerst wat voorbereidend werk doen! Je moet namelijk je vergelijking gaan schrijven in deze vorm:
ax2+bx+c=0
a, b en c noemen we dan coŽfficiŽnten, dat wil zeggen de getallen met a voor het getal in de term met x2, b voor de term met x en c voor het getal.
Voor jouw vergelijking zou dat dan zo gaan:
-2x2 + 20x = 40
Eerst maar eens op nul herleiden:
-2x2 + 20x - 40 = 0
Dan maar eens vereenvoudigen:
x2 - 10x + 20 = 0
We stellen dan vast dat:
a=1 b=-10 en c=20.
Dan pas ga je de ABC-formule invullen. Je krijgt dan:
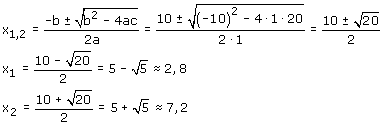
Je ziet: er komt nog al wat bij kijken! Ik weet niet of je dit soort wel foutloos kan doen! Lastige wortels, kwadraten van negatieve getallen.... delen... kortom, het lijkt misschien een handige truuk, maar schiet je er wat mee op?
Bovendien zou ik als docent bij inklemmen vooral ook vergelijkingen geven die je niet met de ABC-formule kan oplossen, maar alleen met inklemmen...
Nogmaals: de abc-formule kan handig zijn, maar alleen als je weet wat je doet, je handig met variabelen kan werken en je je realiseert dat je 'm alleen kan gebruiken bij tweedegraads vergelijkingen...
Hopelijk kan je er iets mee...]
Zie ook 3. ABC formule voor meer voorbeelden.

|
Vragen naar aanleiding van dit antwoord? Klik rechts..!
woensdag 23 februari 2005
|

|



home |
vandaag |
bijzonder |
gastenboek |
statistieken |
wie is wie? |
verhalen |
colofon
©2001-2024 WisFaq - versie 3
|