WisFaq!

De oppervlakte van een figuur met rechthoekige driehoeken

We beginnen met een gelijkbenige rechthoekige driehoek A1 (met rechthoekszijde a), verlengen een rechthoekszijde en brengen daarop een tweede gelijkvormige driehoek A2 aan, waarvan de afmetingen de helft zijn van de eerste (zie figuur). We doen dit opnieuw vanaf Az om Ag te construeren tot in het oneindige. Er ontstäat een soort zaagtandfunctie.

• Bepaal de totale oppervlakte van deze figuur.

Beste kunt u aub mij deze vraag en zijn tussen stappen uitleggen. Ik ben aan het voorbereiden voor het examine. Deze vraag vind ik heel moeilijk.

Riffat
4-12-2020

Antwoord

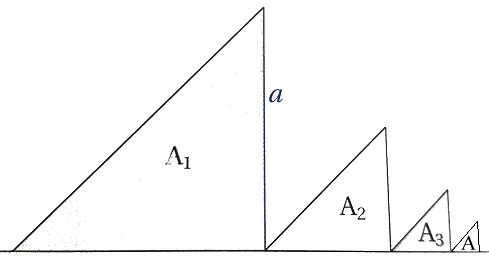
Is de oppervlakte van de opeenvolgende driehoeken niet een voorbeeld van een meetkundige rij?

Dus ik zou denken:

$
\eqalign{
& \frac{1}
{2}a^2 + \frac{1}
{8}a^2 + \frac{1}
{{32}}a^2 + ... \cr
& r = \frac{1}
{4} \cr
& u_0 = \frac{1}
{2}a^2 \cr}
$

Wat is dan de som van de oppervlakte van al die driehoeken?

WvR
4-12-2020