WisFaq!

Re: Driehoek ABC (examenopgave mbo)

Ik heb bij c, de coördinaten van het hoogtepunt uitgerekend. Bij d. weet ik niet wat ik verkeerd doe met de deellijn uit B.

Die deellijn stel ik op (p,q). Als het goed is moet dan in de driehoek gelden (uitgaande van de vectorvoorstellingen):

AB:=(-5,0)+l(2,-1)
BC:=(3,-4)+m(-1,2)

Ik stel het inproduct tussen de deellijn p,q en de richtingsvectoren van AB en BC:

cos$\Phi$₁=(2p-q)/√(5)·√(p²+q²)
cos$\Phi$₂=(-p+2q)/√(5)·√(p²+q²)

Waaruit volgt de richtingsvector (1,1)
En de vectorvoorstelling van de deelijn (3,-4)+e(1,1)
En dus de vergelijking x-y-7=0

Maar het model geeft: x+y+1=0 wat doe ik fout?

mboudd
20-3-2020

Antwoord

Voor de richtingsvector van d neem je de 2 vectoren vanuit B met dezelfde lengte. Daarbij is de richting dus wel van belang!

$
v_d = \left( {\begin{array}{*{20}c}
{ - 2} \\
1 \\
\end{array}} \right) + \left( {\begin{array}{*{20}c}
{ - 1} \\
2 \\
\end{array}} \right) = \left( {\begin{array}{*{20}c}
{ - 3} \\
3 \\
\end{array}} \right)
$



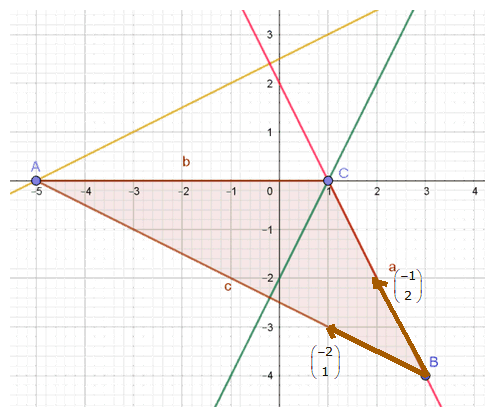
En dan komt het allemaal goed:

$
\begin{array}{l}
d:\left( {\begin{array}{*{20}c}
x \\
y \\
\end{array}} \right) = \left( {\begin{array}{*{20}c}
3 \\
{ - 4} \\
\end{array}} \right) + \lambda \left( {\begin{array}{*{20}c}
{ - 1} \\
1 \\
\end{array}} \right) \\
\left\{ \begin{array}{l}
x = 3 - \lambda \\
y = - 4 + \lambda \\
\end{array} \right. \\
x + y = - 1 \\
x + y + 1 = 0 \\
\end{array}
$

WvR
21-3-2020