WisFaq!

Voor welke waarden is f een stijgende functie?

Gegeven is de functie: f(x)=2x/(2+x²).
Gevraagd: Voor welke waarden is f een stijgende functie?

Als ik f'(x)=0 bereken kom ik uit op x=-√2 en x=√2

...en als ik kijk naar het tekenschema kom ik uit op mbv de quotiëntregel:

(4-2x²)/(2+x²)²=0
x=-√2 v x=√2

Dan zou hij stijgend moeten zijn voor behalve nul:

-√2$<$x$<$0 en 0$<$x$<$√2

Maar ik kan de grafiek niet maken als ik de volgende vragen ook beantwoord:

b) Bereken de extreme waarden van f

Ik heb: minimum: f(-√2)=-¹/₂√2 en
maximum f(√2)=¹/₂√2

c) Bepaal de vergelijking van de horizontale asymptoot van de grafiek van f

Ik heb: lim x$\to\infty$(f(x))=(2/x)/((2/x)+1)=0/(0+1)=0
y= 0 zou dan de horizontale asymptoot moeten zijn , wat ik vreemd vind want hij heeft volgens mij een snijpunt met de x-as: (f(x)=0)
x=0 (0,0) zou dan een snijpunt moten zijn dan kan y = 0 geen horizontale asymptoot zijn.

Hier mee kan d ook niet beantwoorden

d) Teken de grafiek van f.

mboudd
21-9-2019

Antwoord

Volgens mij klopt het bijna allemaal. Je moet alleen niet moeilijk doen over $x=0$. Daar is niets bijzonders mee...

Waarom zou $y=0$ niet een horizontale asymptoot zijn? Daar lijkt me niets mis mee. Je kunt ook nog kijken naar de limiet naar min oneindig. Je vindt dan ook $y=0$ als horizontale asymptoot.

Teken de grafiek maar 's:



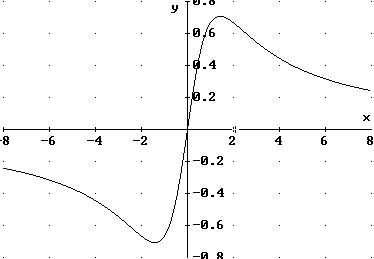
Is het dan duidelijker?

WvR
22-9-2019