Dat gaat zo:
I.
Bij $x-2\ge0$ en $x+1\ge0$ gaat de formule over in:
$f(x)=x-2+x+1=2x-1$ voor $x\ge2$.
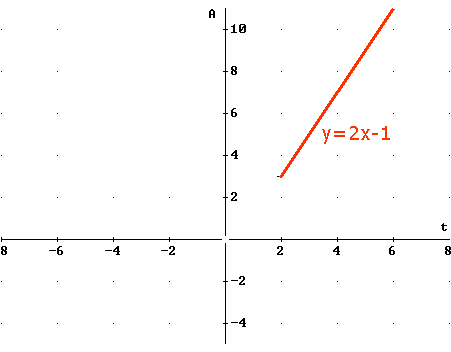
II.
Bij $x-2\ge0$ en $x+1<0$ gaat de formule over in:
$f(x)=x-2-x-1=-3$ voor $x\ge2$ en $x<-1$. Dat kan niet.
III.
Bij $x-2<0$ en $x+1\ge0$ gaat de formule over in:
$f(x)=-x+2+x+1=3$ voor $x<2$ en $x\ge-1$.
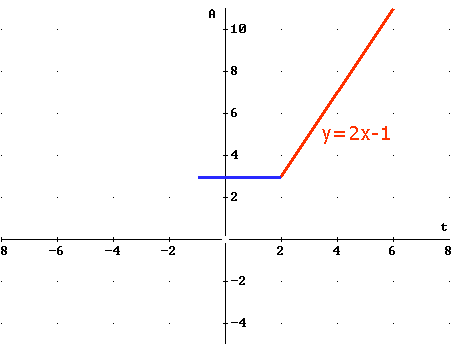
IV.
Bij $x-2<0$ en $x+1<0$ gaat de formule over in:
$f(x)=-x+2-x-1=-2x+1$ voor $x<-1$.
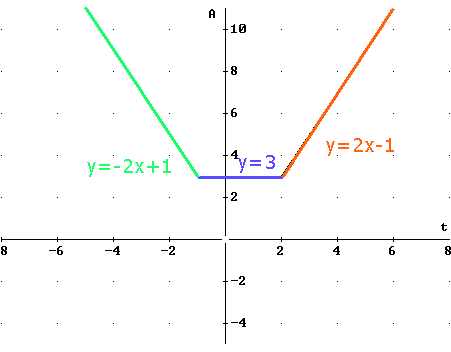
Je vertaalt de voorwaarden naar een nieuw functievoorschrift zonder absoluutstrepen en je bepaalt voor welk interval de nieuwe formule geldt.
Helpt dat?
- Zie ook Functies met absoluutstrepen
WvR
28-10-2018