WisFaq!

Doorsnedes construeren

Ik heb een PO gehad over meetkunde. Hierin moest je alle doorsneden uit een kubus, piramide en cilinder halen en tekenen. Over deze PO moet je nu een toets maken. Je kunt kiezen uit een makkelijke en moeilijke toets, ik heb gekozen voor een moeilijke. Alleen in deze toets moet je doorsneden uit een kubus, piramide of cilinder kunnen construeren. Ik heb dit zelf nog nooit geleerd op school, en heb geen idee waar ik zou moeten beginnen. Ik heb op internet wel constructies gevonden, maar ik snap ze eigenlijk niet. Nu is mijn vraag of jullie misschien de basisbeginselen uit kunnen leggen of een site geven waar ik dit ongeveer kan leren.

Ik zit in 4 VWO.

Alvast hartelijk bedankt!

Sander Spruijt
10-3-2003

Antwoord

Je vraagt nogal wat, maar we gaan een poging wagen...

Laten we eens twee belangrijke stellingen bekijken:

1. Als twee evenwijdige vlakken V en W gesneden worden door een derde vlak U, dan zijn de snijlijnen evenwijdig.

2. Als lijn p van het vlak V de lijn q van het vlak W snijdt in S, dan ligt het snijpunt S van p en q op de snijlijn van de vlakken V en W.
   

Er zijn er meer, maar met deze twee stellingen kan je al heel wat constructies aanpakken.

Ad.1

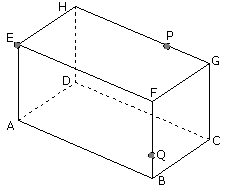
In de balk ABCD.EFGH ligt P op GH en Q op BF. Construeer de doorsnede door E, P en Q.

Uitwerking:

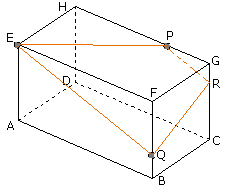
Teken EQ.
Teken PR met PR//EQ (zie stelling 1)



Teken EP en QR



Ad.2
In de balk ABCD.EFGH ligt P op AE, Q op AB en R op BC. Construeer de doorsnede door P,Q en R.


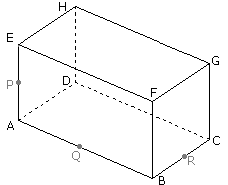
Uitwerking:

Teken PQ
Teken QR
Snijd QR met AD
S is het snijpunt van QR en AD



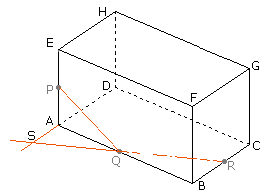
Teken SP. (zie stelling 2)
T is het snijpunt van AP met EH



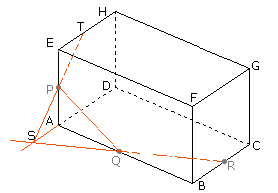
Teken TU//QR (stelling 1)
Teken RV//PT (stelling 1)
Teken UV(//PQ)



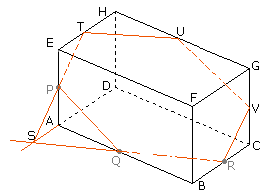
..en zo gaat dat dan. Uiteraard zijn er meerdere wegen die naar Rome leiden.

Ik stel voor dat je eerst bij onderstaande website gaat kijken. Bestudeer de voorbeelden goed en lees de uitleg!

Probeer daarna steeds de doorsneden door de drie punten te tekenen bij deze piramide:

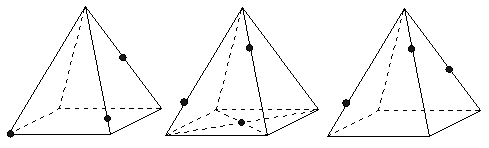
WvR
10-3-2003