WisFaq!

Balk in piramide met een regelmatig achthoekig grondvlak

Er is een regelmatig achthoekige piramide, met zijdes van 60 cm. De hoogte h van de piramide bedraagt 140 cm. In de piramide wordt een balk geplaatst met lengte en breedte x centimeter en hoogte h centimeter.

• Wat zijn de maximale maten van x en h waarvan de balk in de piramide past en wat is de inhoud van die balk met deze waarde van x en h?

Bjorn Buitink
5-11-2015

Antwoord

Hallo Bjorn,

Hieronder heb ik het bovenaanzicht en het vooraanzicht van de piramide getekend, met daarin de grijze balk.



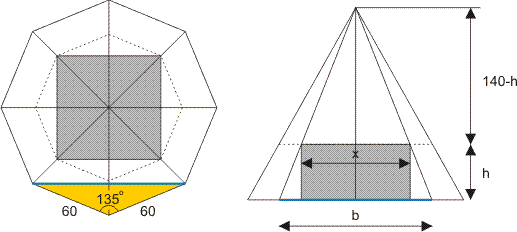
In de figuur rechts zie je:



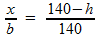
Het blauwe lijnstuk b is een diagonaal van de achthoek, evenwijdig aan een zijde van de balk, zie ook de figuur links.
In deze formule isoleren we h:





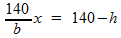
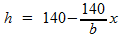
Voor de inhoud I van de balk geldt:



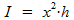
dus:





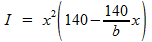
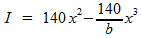
De waarde van b kan je berekenen met behulp van de cosinusregel, toegepast op het gele driehoekje in de linker figuur. Je hebt dan de inhoud I als functie van x. De waarde van x waarbij I maximaal wordt, vind je door de afgeleide van deze functie gelijk te stellen aan nul. Met deze waarde kan je ook de maximale inhoud berekenen.

GHvD
6-11-2015