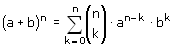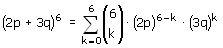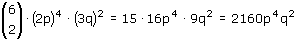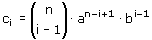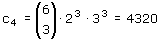WisFaq!

Binomiaalcoëfficiënten

Ten eerste nog bedankt voor de reactie op mijn vorige vraag.Verhelderend.
Helaas heb ik er nog een. Het betreft nu de de driehoek van Pascal.
(a + b)⁶ is een makkie,omdat je dan gebruik kan maken van de driehoek van pascal.

Maar bij het uitwerken van bijvoorbeeld (2p+3q)⁶=64p6+576p5q+260p4q2+4320p3q3+4860p2q4+2916pq5+729q6 reken ik me een ongeluk. Nu heb ik het grote vermoeden dat ook dit veel makkelijker moet kunnen. Iets met veelvouden. Het gaat mij dus om het berekenen van de coefficienten 2 en 3 die uiteindelijk tot 576,260,4320,4860 en 2916 leiden. Allemaal veelvouden van 6, zoals de stap hiervoor allemaal veelvouden van 5 zijn, daarvoor van 4, 3 en 2. Er zit duidelijk regelmaat in,maar welke?

Heeft het iets met de macht te maken?
Alvast hartelijk bedankt.

kees
11-1-2003

Antwoord

Een eerste opmerking is dat die '260' toch wel 2160 zal moeten zijn. Maar hoe bepaal je makkelijk de coëfficiënt van de n-de term?
Laten we dit eens als formule schrijven:



In jouw geval geldt dan dat a=2p, b=3q, dus:



Wil je dan de coëfficiënt weten van de derde term, dan vul je k=2 in:



...en dat is het dan.

In het algemeen zou je kunnen zeggen:
Voor (ax+by)ⁿ geldt voor de i-de coëfficiënt:



Dus bijvoorbeeld de coëfficiënt van de 4de term in je voorbeeld:
a=2, b=3, i=4 levert:

WvR
12-1-2003