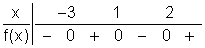WisFaq!

Bepaal het tekenverloop

Hoi,

Zoals de titel al zegt, moet ik het tekenverloop bepalen van de functie (x-1)(x-2)(x+3). Ik weet dat een voorschrift van een tweedegraads functie ax² +bx +c is. Mijn vraag is dus of iemand mij kan vertellen hoe ik hieraan moet beginnen en hoe ik het tekenverloop schema moet opstellen. Graag alles uitleggen :D

Ili
28-5-2011

Antwoord

Het lastigste werk is al voor je gedaan, namelijk de veelterm is al ontbonden in factoren. Wat je nu moet doen is voor elk van de factoren afzonderlijk het tekenverloop opstellen (het zijn allemaal rechten, dus dat is niet zo moeilijk) en daarna concluderen wat het teken van de originele functie is, (+ maal + is +, + maal - is -, - maal - is +)

Bijvoorbeeld: tekenverloop van f(x) = (x+3)(4-x)

Het tekenverloop van (x-3) is (nulpunt = -3 en de rechte is stijgend)

x           -3

x+3      ----0++++

Het tekenverloop van (4-x) is (nulpunt = 4 en de rechte is dalend)

x            4

4-x      ++++0----

In een gecombineerd overzicht wordt dat

x                -3      4

x+3          ----0++++++++++++
4-x          ++++++++++++0----

(x+3)(4-x)   ----0+++++++0----

waarbij het laatste volgt uit de de produktregel voor tekens die ik hierboven al aanhaalde. Lukt het zo?

cl
29-5-2011