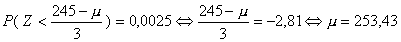WisFaq!

De kromme van Gauss

Heb hier een opgave dat met kromme van gaus te maken heeft. Nu begrijp ik die kromme niet en hoop ik dat jullie ook hier weer een antwoord op hebben.

Het netto-gewicht van pakjes boter is normaal-verdeeld met een standaarddeviatie van 3 g. Als een pakje bij controle door de keuringsdienst van waren een gewicht van minder dan 245 g blijkt te hebbewn krijgt de fabrikant een boete.
Op welk gemiddelde m moet de fabrikant de verpakkingsmachine afstellen om het risico van een boete tot 0,25 % te beperken?

jurgen
17-6-2003

Antwoord

X is het gewicht van een pakje boter, X is normaal verdeeld met gemiddelde m (onbekend) en standaarddeviatie s = 3.
Nu weet je dat de kans op een pakje met minder dan 245 gram 0,0025 is. Dat betekent P(X 245) = 0,0025 nu eerst standaardiseren:

Die -2,81 is de grenswaarde die je krijgt als je die kans 0,0025 met een tabel of een GR terugzoekt.
De Gauss kromme gebruik je dus niet echt, die komt alleen maar om de hoek kijken bij het opzoeken van de grenswaarde.

Met vriendelijke groet

JaDeX

jadex
17-6-2003