Om het gemiddelde van een aantal getallen te berekenen tel je alle getallen op en deel je de som door het aantal. Voor het steekproefgemiddelde gebruiken we de notatie $\overline x$ en voor het populatiegemiddelde de notatie µ.
Voorbeeld
Je hebt 6 pakken koffie gewogen.
De gewichten in gram zijn: 245, 255, 256, 249, 250 en 251.
Het gemiddelde is:
$\Large\frac{245+255+256+249+250+251}{6}$=$251$
Voorbeeld
|
leeftijd in jaren |
frequentie |
|
12 |
5 |
|
13 |
12 |
|
14 |
28 |
|
15 |
16 |
|
16 |
5 |
Bereken de gemiddelde leeftijd van deze groep leerlingen.
Uitwerking
$\large\frac{12,5\cdot 5+13,5\cdot 12+14,5\cdot 28+15,5\cdot 16+16,5\cdot 5}{66}$=$14.56$
Om het gemiddelde uit te rekenen moet je bij frequentietabellen altijd de klassemiddens gebruiken. Je gaat er als het ware van uit dat het klassemidden van een klasse het gemiddelde van die klasse is.
Hier gaat het om leeftijd! Mensen van 15 jaar oud variëren in leeftijd van 15 tot (net geen) 16 jaar oud. Dus het klassemidden is 15,5.
Formule
Als formule kan je de berekening als volgt noteren:
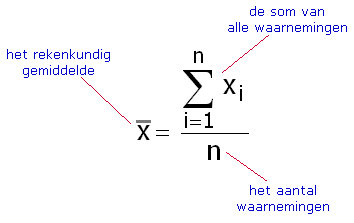
Extra
Het gemiddelde is erg gevoelig voor uitschieters. Men spreekt in dit verband wel van een niet resistente maat van het centrum.
Voorbeeld:
Een leerling haalt voor de toetsen 4 keer een 6 en één keer een 1. Het gemiddelde is nu 5. Dit zou kunnen leiden tot een onvoldoende op het rapport. Dat lijkt niet erg eerlijk. Deze leerling beheerst de stof voor 80% voldoende.
Een andere leerling haalt 2 keer een 4 en 2 keer een 5 en één keer een 10. Gemiddeld is dat 5,6 en misschien wel een 6- op het rapport. Deze leerling beheerst slechts 20% van de stof voldoende.

Hoe twee marktkooplui ruzie krijgen
Op de Albert Cuypmarkt zijn er twee marktkooplui die allebei 120 appels verkopen. De een verkoopt ze voor 50 cent en de ander verkoopt er drie voor een gulden. Samen hebben ze een opbrengst van 60 + 40 = 100 gulden. Gemiddeld verkopen ze (2+3)/2=2,5 appel voor 1 gulden. Ze besluiten samen te werken. Halve appels verkopen ze niet. Ze besluiten 5 appels te verkopen voor 2 gulden.
Aan het eind van de dag zijn alle appels verkocht. Ze tellen de opbrengst die 96 gulden blijkt te zijn. Ze gaan op zoek naar de ontbrekende 4 gulden en beschuldigen elkaar ervan het ingepikt te hebben. Je begrijpt dat ze de volgende dag weer ieder apart hun appels verkopen. Wat hebben ze over het hoofd gezien?
http://www.science.uva.nl/misc/pythagoras/rubriek/fallacy/markt/
Van A naar B
Een wiskundedocent reist van A naar B. Zijn gemiddelde snelheid daarbij is precies 50 km/uur. Hoe lang moet de wiskundedocent over de terugreis doen om gemiddeld over de heen- en terugreis op 100 km/uur uit te komen?








