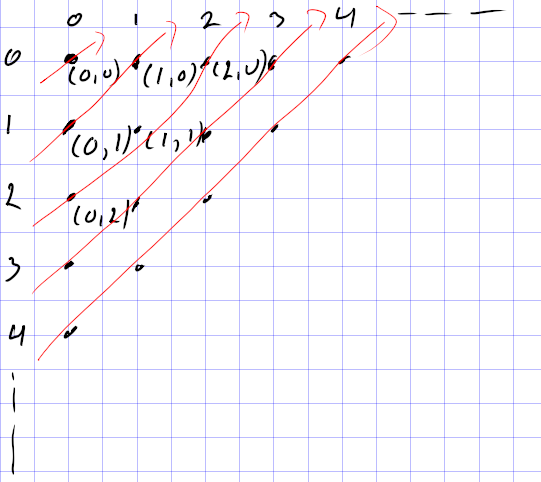WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Verzamelingen

Functies

Begrijp ik niet:

stel f:X $\to $ X, A $\subset $ X, dan
A $\subset $ f^-1(f(A))

Voorbeeld:
A={1,2,4,7}
f(A) = {2,4}
f^-1(f(A))={1,2}

A is hier toch geen deelverzameling van, maar omvat f^-1(f(A))={1,2}
Geys F
27-1-2024

Antwoord

Je voorbeeld zegt niets want je geeft niet aan wat $X$ is en wat de werking van de afbeelding $f:X\to X$ is.
Maak maar een $X$ en een $f:X\to X$ met $A=\{1,2,4,7\}\subset X$ en zo dat $f[A]=\{2,3\}$ en ook nog zo dat $f^{-1}[f[A]]=\{1,2\}$. Het zal je niet lukken, want $\dots$

Als je naar de definities kijkt wordt duidelijk dat de inclusie wel degelijk geldt.
Eerst de definities:
$f[A]=\{f(a):a\in A\}$
$f^{-1}[B]=\{x:f(x)\in B\}$
Dus $x\in f^{-1}[f[A]]$ betekent $f(x)\in f[A]$.
Welnu, als $a\in A$ dan, per definitie, $f(a)\in f[A]$, en dus, per definitie, $a\in f^{-1}[f[A]]$.
Conclusie: voor alle $a\in A$ geldt $a\in f^{-1}[f[A]]$, ofwel $A\subset f^{-1}[f[A]]$.
kphart
27-1-2024

Gelijkmachtigheid en kardinaalgetal

Ik zit in de knoei met gelijkmachtigheid en kardinaalgetal.
Twee verzamelingen zijn gelijkmachtig indien er een bijectie tussen beide bestaat
De relatie 'is gelijkmachtig met' is een equivalentierelatie
De equivalentieklassen noemen we de kardinaalgetallen van de verzameling
Wel: neem nu de verzameling van de natuurlijke getallen met de relatie van y = 2x. Dan heb ik twee verzamelingen die gelijkmachtig zijn, nl. $\mathbf{N}$ en $\mathbf{N}$ X $\mathbf{N}$ door de relatie. Dan is het kardinaalgetal van $\mathbf{N}$ gelijk aan het kardinaalgetal van $\mathbf{N}$ /R, nl. aleph

Maar hoe moet ik die equivalentierelatie (reflexief, symmetrisch en transitief) en equivalentieklassen zien?
Geys F
1-2-2024

Antwoord

Het helpt als je de definities op je in laat werken.
De definitie van gelijkmachtig is in orde
Dat de relatie "is gelijkmachtig met" een equivalentierelatie is klopt, maar hou ik de gaten dat het een relatie tussen verzamelingen is
je volgende zin lijkt een (ongeoorloofde) mix van twee losse zinnen
de eerste is: "de equivalentieklassen noemen we kardinaalgetallen"
de tweede is: "het kardinaalgetal van een verzameling is de equivalentieklasse waar deze toe behoort"
Daarna gaat het helemaal mis: de relatie "$y=2x$" heeft niets met de bovenstaande relatie van gelijkmachtigheid te maken: je hebt zomaar wat opgeschreven. Tenzij je met "$y=2x$" iets bedoelt wat ik niet zie.
De relatie is in ieder geval geen equivalentierelatie op $\mathbb{N}$ dus equivalentieklassen levert hij ook niet op.

Het antwoord op je vraag, als we het over "$y=2x$" hebben, is: het is geen equivalentierelatie en er zijn geen equivalentieklassen.

Overigens: er is een bijectie tussen $\mathbb{N}$ en $\mathbb{N}\times\mathbb{N}$ (probeer er maar een te maken) dus die twee verzamelingen zijn gelijkmachtig en bepalen dezelfde equivalentieklasse; in die klasse zitten ook de verzamelingen van gehele getallen, van rationale getallen, de algebraïsche getallen, en nog veel meer.
kphart
1-2-2024

Kardinaliteit

In mijn vrije tijd doe ik soms wat wiskunde, deze keer dacht ik aan Cantor met zijn bewijs dat |ℕ| = |ℚ| $<$ |ℝ| (waar |A| de kardinaliteit van A voorstelt); Nu dacht ik: 'Je kunt breuken voorstellen als tweedimensionale coördinaten in de vorm (a, b), wat zou de kardinaliteit dan zijn van een verzameling met coördinaten in de vorm (a, b, c)?' Ik denk dat dit ook ℵ₀ is maar weet niet hoe ik dit kan bewijzen. Kan men ook bewijzen dat de kardinaliteit van een verzameling met elementen in de vorm (a, b, c, d, ...) (met n coördinaten) ook ℵ₀ is voor alle n?
Oliver
5-5-2024

Antwoord

1. Dat kan inderdaad. We nemen even $\mathbb{N}=\{0,1,2,3,4,5,\ldots\}$ want dan werkt de volgende formule (van Cantor zelf) heel mooi.
Geef dan het paar $(a,b)$ het nummer $\frac12(a+b)(a+b+1)+a$. Reken de eerste nummers maar uit: $(0,0)\to0$, $(0,1)\to1$, $(1,0)\to2$, $(0,2)\to3$, $(1,1)\to4$, $(2,0)\to5$, enzovoort.

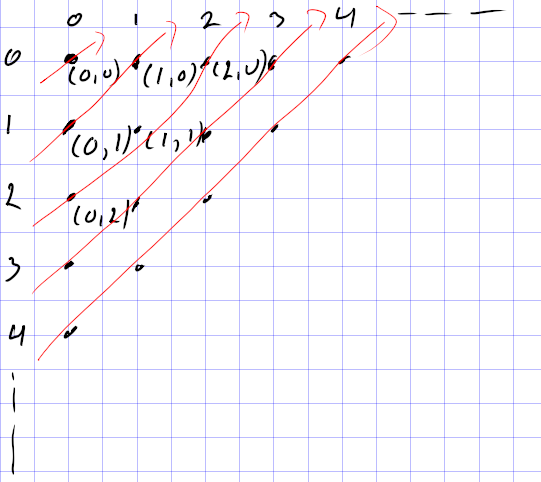
In het plaatje lopen de nummers op elke lijn van links naar rechts.
Dit levert een bijectie tussen de paren naturlijke getallen en de natuurlijke getallen zelf.

2. Ook dat kan. We schrijven $f(a,b)=\frac12(a+b)(a+b+1)+a$. Maak nu van elk drietal een tweetal: $(a,b,c)\to\bigl(f(a,b),c\bigr)$. Dat is een bijectie tussen de drietallen en de paren.

Op dezelfde manier kun je laten zien dat er evenveel $(n+1)$-tallen zijn als $n$-tallen.
kphart
5-5-2024