|
|
|
\require{AMSmath}
Ruimtemeetkunde
Mantel afgeknotte kegel
Graag zou ik willen weten hoe het volgende werkt:
Ik heb een afgeknotte kegel met hoogte 135 mm, bovendiameter 85, onderdiameter 65 mm. Hier moet een sleeve/mantel omheen met een hoogte van 105mm, en deze moet in het midden om de afgeknotte kegel heen sluiten.
Ik vermoed dat de s, r en $\theta $ van de afgeknotte kegel berekenen helpt bij het maken van de uitslag van de sleeve/mantel, maar ik kom niet verder met het doorrekenen naar hoogte-aanpassingen, omdat dan de diameters veranderen.
Julia
4-1-2024
Antwoord

Bekijk het volgende plaatje
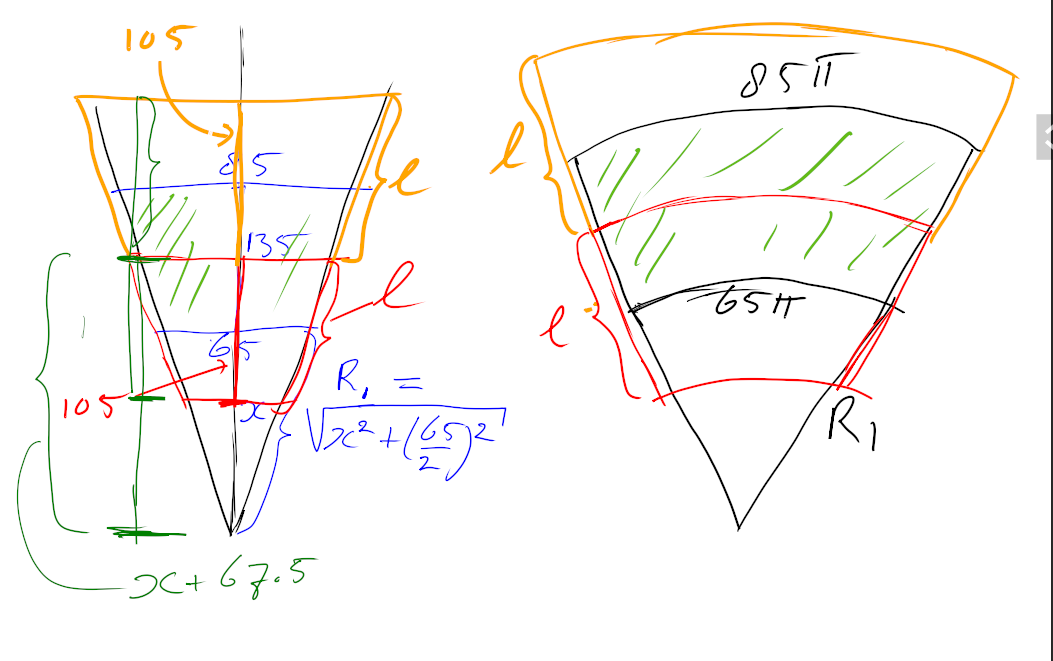
Daarin heb ik (schematisch) de afgeknotte kegel getekend en ik heb hem volledig gemaakt tot de top. Het getal $x$ is de hoogte van het toegevoegde stuk. Wegens gelijkvormigheid moet gelden dat $x:65 = (x+135):85$, daaruit leidt je af dat $x=438.75$ (alles in $\mathrm{mm}$ natuurlijk). Voor de uitslag moet je $R_1$ weten en die is gelijk aan $\sqrt{x^2+(65/2)^2}$ (Pythagoras) en dat is ongeveer $439.95$. In de uitslag rechts zie je de sector (taartpunt) met straal $R_1$ en booglengte $65\pi$ (de lengte van de cirkel bij diameter $65$).
Je sleeve moet in het midden aansluiten maar je schreef niet aan welke kant; ik heb beide mogelijkheden maar getekend: rood naar de punt toe, oranje van de punt af. Het midden ligt op hoogte $x+135/2=x+67.5$.
De diameter halverwege je afgeknotte kegel is gelijk aan $75$, met gelijkvormigheid volgt dat dat de straal van de rode boog in de uitslag (in het groene gebied) gelijk is aan $\eqalign{\frac{75}{65}R_1}$.
Ten slotte moet je $\ell$ nog weten; dat gaat weer met gelijkvormigheid:
$\ell:105=R_1:x$, dus $\eqalign{\ell=\frac{R_1}{105}x}$.
kphart
5-1-2024
Korste weg tussen twee punten
Ik heb een vraag over hoe je de kortste weg tussen twee punten moet berekenen op een balk. Ik zag al dat deze vraag was beantwoord en had ook de manieren toegepast van wat erin stond, maar de docent zei telkens dat het antwoord 40 was en geen 42. Daarom vraag ik hierbij voor hulp.
De vraag is:
Een beer leeft op een balkvormige planeet van 12 x 12 x 30 eenheden (hieronder een plaatje ervan). Op dit moment bevindt de beer zich in punt B op het rechterzijvlak van de planeet. Zijn pot honing bevindt zich in punt H op het linkerzijvlak van de planeet. De beer heeft honger, maar hij wil geen onnodige energie verspillen. Daarom vraagt hij zichzelf af wat de kortst mogelijke weg is van zijn plek naar de honing. Ofwel, van punt B naar punt H.
Milad
2-4-2024
Antwoord

Hallo Milad,
Handig is om een uitslag van de balk te tekenen. Met een rechte lijn kan je dan een route voor de beer tekenen en de lengte van de route berekenen. Jij dacht waarschijnlijk aan deze uitslag:
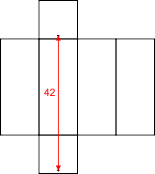
De afstand tussen de punten B en H is 42 eenheden. Maar je kunt ook aan andere uitslagen denken, waarmee je andere routes kunt doorrekenen. Wat dacht je bijvoorbeeld van de onderstaande routes:
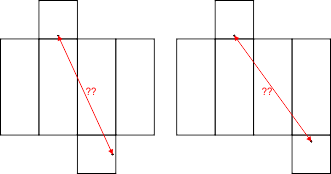
Bereken in deze uitslagen maar eens de lengte van de aangegeven route en laat je verrassen ...
GHvD
2-4-2024
Manteloppervlakte van een kegel en afgeknotte kegel
Gegeven is een kegel met straal r, hoogte h en apothema a. Op een afstand x van de top brengt met een vlak aan evenwijdig met het grondvlak. Bepaal x zodat de oppervlakte van de doorsnede gelijk is aan de zijdelingse oppervlakte van de afgeknotte kegel die ontstaat.
Kan er iemand dit uitleggen.
Jozef
28-4-2024
Antwoord

Maak een plaatje.
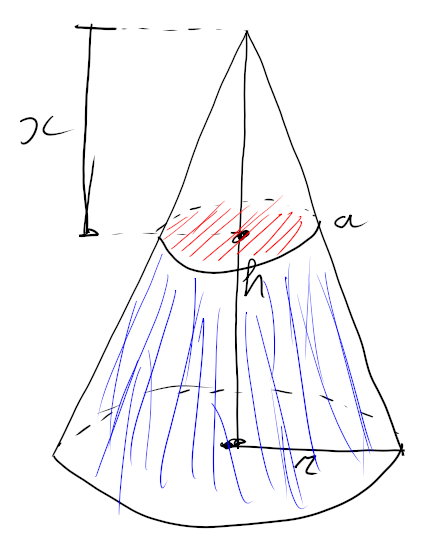
Het lijkt me dat de vraag is $x$ zo te kiezen dat de rode schijf en blauwe mantel dezelfde oppervlakte hebben.
Voor de schijf moet je de straal $s$ uitdrukken in $x$. Gebruik daarbij dat $x:s=h:r$ wegens gelijkvormigheid van driehoeken.
De oppervlakte van de mantel kun je uit de bekende formules halen. Je krijgt een vergelijking in $x$ op te lossen.
kphart
29-4-2024
Re: Doorsnede construeren van een vlak met een zeshoekige piramide
Ik snap niets van deze uitleg. Eerst geef je lijn RS, vervolgen na een stap vind je punt S? En de rest gaat even zo?
c. can
20-5-2024
Antwoord

Er staat uitgelegd hoe je met behulp van de lijn k het punt S kan vinden dus zo vreemd is dat niet:
Dat gaat zo: teken de snijlijn van de vlakken ABT en CDT. Dat is de lijn k. De lijn PQ en RS snijden elkaar op k (waarom eigenlijk?). Daarmee kan je dan punt S vinden.
Lukt het dan?
In onderstaand artikel kan je meer uitleg vinden. Er is er ook een werkblad bij:Voor de liefhebbers heb ik ook nog een uitwerking van de opdrachten uit het werkblad in de aanbieding. Je kunt reageren op dit bericht.
WvR
20-5-2024
Langste kortste weg tussen twee punten
Hallo,
Ik heb een vraag. Hoe bereken je de langste weg op een balk? Ik kon helaas geen bronnen vinden over hoe je de langste weg moet vinden, maar wel over hoe je de kortste weg moet vinden.
Ik bedoel ook niet letterlijk de langste weg tussen twee punten, aangezien het oneindig kan zijn, maar eigenlijk eerder de langste kortste weg als je het begrijpt. Het moet de langst mogelijke weg zijn tussen twee punten, maar het moet ook een rechte lijn zijn.
Alvast bedankt,
Mvg,
Milad 
Milad
29-5-2024
Antwoord

Hallo Milad,
Wellicht heb je de vraag kortste weg tussen twee punten in gedachten. Hierbij is het de bedoeling om de kortste weg tussen de punten B en H te vinden over de zijden van een balk:

Zoals je in het antwoord kunt lezen, is het een kwestie van uitslagen tekenen om de kortste, dus rechte lijn te vinden tussen de twee punten.
Je merkt terecht op dat er geen langste weg bestaat, want onderweg kan je oneindig lang in rondjes draaien. Maar er is ook geen langste rechte weg, zoals je in onderstaande figuur kunt zien:

Je kunt in een rechte lijn meerdere keren rond de balk lopen. Als je de wikkelingen maar dicht genoeg bij elkaar legt, wordt de route ook onbegrensd lang.
Wellicht bedoel je dat je maar één keer over elk vlak mag lopen. In dat geval is het, net als bij het vinden van de kortste route, een kwestie van uitproberen. Teken meerdere uitslagen, trek een rechte lijn tussen de punten B en H en bereken met Pythagoras de lengte van deze lijn. Hieronder heb ik enkele mogelijke uitslagen getekend:

GHvD
29-5-2024
Re: Langste kortste weg tussen twee punten
Hallo Gilbert,
Bedankt voor het antwoorden van mijn vraag, alleen denk ik dat ik de vraag een beetje onduidelijk heb gesteld.
Ik wil namelijk de langste weg weten op een balk. Hiermee bedoelde ik niet perse de weg tussen punt B en H, aangezien ik die antwoorden al had.
Ik bedoel eigenlijk wat de langst mogelijke weg is op een balk. Je kan bijvoorbeeld van helemaal linksonder naar rechtsboven een lijntrekken en dat de langst mogelijke weg noemen, maar dat is niet per se mogelijk, aangezien rechtsboven en linksboven hetzelfde punt is.
De balk die u in principe had gebruikt is wel goed, maar helaas had ik de vraag niet helemaal goed gesteld.
Sorry voor het ongemak,
Alvast Bedankt,
Mvg,
Milad Herawi

Milad
30-5-2024
Antwoord

Hallo Milad,
Als ik het goed begrijp, zoek je eigenlijk hoe je twee punten B en H op een balk kunt kiezen, zodanig dat de kortste afstand tussen deze punten zo groot mogelijk is (afstand over de zijvlakken van de balk). Dat is een puzzel die je op dezelfde manier kunt aanpakken als bij de vorige vragen: teken diverse uitslagen van de balk, bekijk hoe je twee punten kunt kiezen die zo ver mogelijk van elkaar verwijderd zijn, en bereken de afstand tussen die punten met Pythagoras. Je moet alleen wel steeds controleren of er geen kortere route mogelijk is wanneer je de uitslag weer tot een balk vouwt.
In onderstaande figuur lijkt de afstand tussen de punten B en H heel groot:

Maar na vouwen van de balk blijken deze punten niet zo ver van elkaar te liggen, zie de linker figuur hieronder. Je kunt dit zien door dezelfde punten op een andere uitslag van de balk te tekenen:

Ik zou zeggen: teken diverse mogelijke uitslagen van een balk (er zijn niet heel veel mogelijkheden), kies op een uitslag twee punten die ver van elkaar (lijken te) liggen. Zoek uit waar deze punten in de andere uitslagen liggen, en kijk of in een andere uitslag geen kortere afstand te vinden is. Zo moet je, na enig puzzelen, wel tot de 'langste kortste route' kunnen komen.
Laat maar weten wat de langste route is die jij kunt vinden.
GHvD
30-5-2024
Re: Afstand van twee lijnen
Graag een illustratie.
Pelswi
4-7-2024
Antwoord

Hier is een tekening.

kphart
9-7-2024



home |
vandaag |
bijzonder |
gastenboek |
statistieken |
wie is wie? |
verhalen |
colofon
©2001-2024 WisFaq - versie 3
|






















