WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Kansrekenen

Draaien aan een rad

Als ik 1x aan een rad draai met 31 mogelijke getallen is de kans dat deze op mijn getal komt 3,9%.
Hoeveel is dat als ik 4 pogingen krijg om 1x van de 4 op mijn getal terecht te komen?

stefan
29-2-2024

Antwoord

Er zijn twee gebeuertenissen als je aan het rad draait:

A: het rad komt op jouw getal
B: het rad komt niet op jouw getal

Er zijn dan 4 verschillende mogelijkheden als je 4 keer draait en het rad precies 1 keer op jouw getal komt:

ABBB
BABB
BBAB
BBBA

De kanssn op deze mogelijke uitkomsten zijn steeds gelijk aan:

$
\eqalign{\frac{1}
{{31}} \cdot \left( {\frac{{30}}
{{31}}} \right)^3}
$

Dus de totale kans is:

$
\eqalign{P({\text{1xA en 3xB}}) = 4 \cdot \frac{1}
{{31}} \cdot \left( {\frac{{30}}
{{31}}} \right)^3 \approx 0,117}
$

Helpt dat?

Aanvulling

Je kan het kansexperiment opvatten als een binomiaal kansexperiment:

"In het geval van n waarnemingen, alle onafhankelijk, elk resulterend in succes of mislukking, en elk met eenzelfde kans $p$ op succes, spreekt men van een binomiale kansverdeling."

Zie 3. Binomiale verdeling

Helpt dat?

Naschrift

Je kunt ook doorrekenen met $0,039$ maar dat is dan wel afgerond. Je eindantwoord wordt dan wel erg onnauwkeurig!

$
\eqalign{P({\text{1xA en 3xB}}) = 4 \cdot 0,039 \cdot \left( {1 - 0,039} \right)^3 \approx 0,138}
$

Ik zou dat niet goed vinden...
WvR
29-2-2024

Patience: hoeveel kansen dat ik alle 52 kaarten ineens kan uitleggen?

hoeveel kansen dat ik zonder onerbreking alle 52 komleg?aarten

Guido
13-3-2024

Antwoord

Hallo Guido,

Eigenlijk is hier geen sprake van een wiskundige kans, omdat je als speler (soms) keuzes kunt maken. Een bepaalde kaart kan je bijvoorbeeld op twee verschillende plekken leggen, of je kunt ervoor kiezen om een kaart wel of niet weg te leggen. Hiermee heeft de speler invloed op het al dan niet uitkomen van het spel.

Je zou kunnen afspreken dat je elke mogelijkheid om een kaart weg te leggen altijd moet benutten, en dat je bij twee mogelijkheden bijvoorbeeld altijd de meest linker mogelijkheid kiest. Het spel is dan wel eenduidig, maar gezien het enorme aantal mogelijkheden dat zich kan voordoen, lijkt het me onbegonnen werk om via de wiskunde een theoretische kans te berekenen dat het spel uitkomt. Meer voor de hand ligt dan om een simulatieprogramma te maken en deze kans empirisch te bepalen.
GHvD
18-3-2024

Venndiagram

Is dit beide waar?

P(A or B)= P(A) + P(B) - P(A and B)
P(A and B)= P(A) + P(B) - P(A or B)

Hoe heten deze regels, en waar kan ik meer info vinden hierover online?
Marty
2-4-2024

Antwoord

Ja, die kloppen allebei en ze zijn equivalent aan
$$
P(A)+P(B) = P(A\mathbin{\text{or}} B)+P(A\mathbin{\text{and}} B)
$$
Kijk naar het onderstaande plaatje, waar ik `or' vervangen heb door $\cup$ (vereniging) en `and' door $\cap$ (doorsnede).

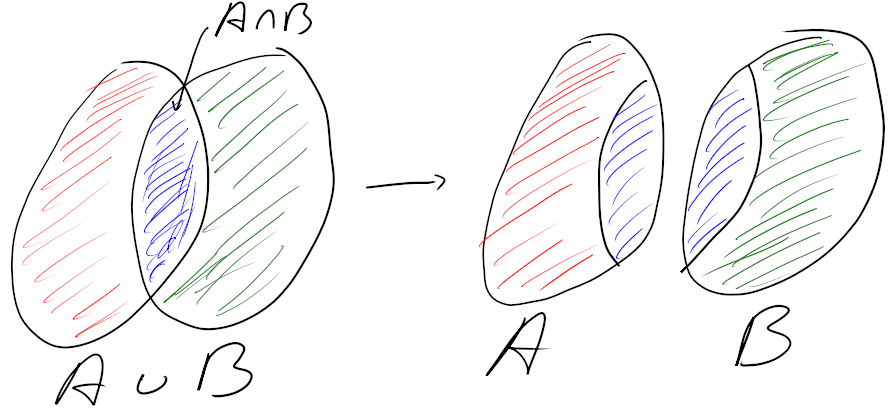
Rechts zie je $A$ en $B$ losgemaakt van elkaar, het blauwe stuk is de doorsnede (het `en'-gedeelte) en dat wordt twee keer geteld als je $P(A)+P(B)$ bepaalt.
In $P(A\cup B)$ worden de drie stukken elk één keer geteld dus moet je bij $P(A\cup B)$ nog $P(A\cap B)$ optellen om $P(A)+P(B)$ te krijgen.

Over kansrekening en wat daarmee samenhangt zijn veel boeken te vinden, bijvoorbeeld Kansrekening van Alex van den Brandhof (als je op die site naar `Kansrekening zoekt vindt je nog meer boeken).

kphart
2-4-2024

Drie dobbelstenen

Je hebt drie dobbelstenen, waarmee je een keer gooit. Het totaal aantal ogen van deze worp onthoud je. Hierna gooi je deze drie dobbelstenen nóg een keer, telt weer het aantal ogen bij elkaar op en vermenigvuldigt dit totaal met de uitkomst van de eertse worp.

Wat is de kans op een uitkomst kleiner dan honderd?
J van
18-6-2024

Antwoord

Hallo J,

Deze vraag is zeer geschikt voor nog eens een regenachtig weekend ...
Maak eerst een kansverdeling van het totaal aantal ogen wanneer je met drie dobbelstenen gooit. Dat wil zeggen: bereken voor elk mogelijk aantal ogen de kans dat dit optreedt. Ik geef enkele voorbeelden:

3 ogen:
De enige mogelijkheid om dit te bereiken, is drie keer een 1 gooien. De kans op drie ogen is ¹/₆·¹/₆·¹/₆ = ¹/₂₁₆

6 ogen:
Dit kan o.a. worden bereikt met de combinatie 1, 1, 4. Dit kan op 3 manieren, want de 4 kan door drie verschillende dobbelstenen worden gegooid. De kans op twee keer 1 en één keer 4 is zodoende ¹/₆·¹/₆·¹/₆·3 = ³/₂₁₆.

Je bereikt dit ook met de combinatie 1, 2, 3. Dit kan op 6 manieren: 3 mogelijkheden voor de 1, dan nog 2 mogelijkheden voor de 2, dan ligt de 1 vast. Zoedoende zijn er 3·2=6 mogelijkheden. De kans op een 1, een 2 en een 3 is dan ¹/₆·¹/₆·¹/₆·6 = ⁶/₂₁₆.

Tot slot kan je aan 6 ogen komen met 3 keer een 2. Dit kan maar op één manier, deze kans is dus ¹/₆·¹/₆·¹/₆ = ¹/₂₁₆.
De totale kans op 6 ogen komt hiermee op ³/₂₁₆+⁶/₂₁₆+¹/₂₁₆ = ¹⁰/₂₁₆.

Doe hetzelfde voor alle mogelijke uitkomsten, dus 3 t/m 18 ogen. Je zult zien dat het berekenen van de kans op 10 of 11 ogen het meeste rekenwerk vraagt. Voor beide aantallen geldt dat dit aantal op 27(!) manieren bereikt kan worden, waarmee voor beide aantallen de kans op ²⁷/₂₁₆ komt.

Je eindigt met een tabel met daarin het aantal ogen en de bijbehorende kans, in 216-sten. Een deel van deze tabel zie je hieronder:

Maak nu nog een tabel (rooster) waarin je horizontaal de ogen van de eerste worp uitzet (dus 3 t/m 18) en verticaal de ogen van de tweede worp (weer 3 t/m 18). Een deel van deze tabel zie je hieronder:

In elke cel noteer de de kans dat deze combinatie van eerste en tweede worp optreedt. Ik geef drie voorbeelden:
De kans op 3 ogen is ¹/₂₁₆, daarmee komt de kans op 3 ogen in de eerste worp èn 3 ogen in de tweede worp op ¹/₂₁₆·¹/₂₁₆=¹/₄₆₆₅₆. In cel (3 , 3) noteer je deze kans 1 (kans in 46656-sten).
De kans op 'eerste worp 3 ogen en tweede worp 6 ogen' is ¹/₂₁₆·¹⁰/₂₁₆=¹⁰/₄₆₆₅₆. In cel (3 , 6) noteer je dus 10. Ook in cel (6 , 3) noteer je 10, want deze kans is hetzelfde.

In cel (6 , 6) noteer je 100, want de kans op 'eerste worp 6 en tweede worp 6' is ¹⁰/₂₁₆·¹⁰/₂₁₆=¹⁰⁰/₄₆₆₅₆.

Zo eindig je met een tabel met de kansen op elke mogelijke worp, in 46656-sten. Tel tot slot alle waarden op van cellen die behoren bij worpen waarbij het product kleiner is dan 100. Dit totaal, gedeeld door 46656, levert de gevraagde kans.

Tip 1: zet eerst een kruis in cellen die overeenkomen met worpen met een product van minstens 100, zoals (18 , 6) t/m (18 , 18). Dat scheelt rekenwerk.

Tip 2: gebruik een spreadsheet waarmee je veel berekeningen kunt automatiseren.
Ik kom hiermee op een kans van wat minder dan een half. Jij ook?
GHvD
18-6-2024

Voorwaardelijke kans

Er werd een onderzoek opgezet naar de werkzaamheid van een nieuwe test voor het opsporen van een parasiet op beukenbomen. Elke beuk reageert positief of negatief op de test.
De bevindingen van het onderzoek zijn de volgende:
14% van de beuken test positiet,
2% van de beuken test positief, maar heeft de parasiet niet,
4% van de beuken test negatief, maar heeft toch de parasiet.
Wat is de kans dat, als een beuk de parasiet heeft, de beuk ook positief zal testen?
Sirine
24-6-2024

Antwoord

Hallo Sirine,

Zet de gegevens in een kruistabel:

De lege cellen kan je nu berekenen, bijvoorbeeld:
14% test positief, dus 100-14=86% test negatief. In de cel tussen 14 en 100 noteer je dus 86. Vul op deze manier de tabel helemaal in.

Dan de kans dat, als een beuk de parasiet heeft (dus: 16%), de beuk ook positief zal testen (dat is 12%). Deze kans is zodoende ¹²/₁₆.

OK zo?
GHvD
25-6-2024

Een gezin van vier

Kans op een jongen is 51 procent , hoe groot is de kans dat een gezin van vier kinderen 4 jongens heeft als je weet dat ze 4 kinderen van hetzelfde geslacht hebben?
Esmee
25-6-2024

Antwoord

Hallo Esmee,

De kans op 4 jongens is 0,51⁴. De kans op 4 kinderen van hetzelfde geslacht is 0,51⁴+0,49⁴ (begrijp je waarom?). Deel deze kansen door elkaar om de kans op 4 jongens te vinden, onder de voorwaarde dat de 4 kinderen van hetzelfde geslacht zijn.
GHvD
25-6-2024

Re: Een gezin van vier

Bedankt! Het antwoord schijnt 53,99% te zijn, maar ik weet niet hoe ik dit zou moeten berekenen, ook niet met deze extra uitleg. Je weet dat het of 4 jongens zijn of 4 meisjes. Heel eerlijk gezegd zou ik denken dat de kans 51% is omdat de kans op jongens 51% is en op meisjes 49%.
Esmee
25-6-2024

Antwoord

Hallo Esmee,

De kans op een jongen is 0,51. De kans op twee jongens is 0,51 $\times $ 0,51=0,2601, enz. De kans op 4 jongens is 0,51⁴ $\approx$ 0,06765.
Op dezelfde manier vind je: de kans op 4 meisjes is 0,49⁴ $\approx$ 0,05765.

Stel dat je 10000 gezinnen beschouwt met 4 kinderen. Dan verwacht je:
Aantal gezinnen met 4 jongens: 0,06765 $\times $ 10000=6765 gezinnen
Aantal gezinnen met 4 meisjes: 0,05765 $\times $ 10000=5765 gezinnen

Totaal aantal gezinnen met 4 kinderen: 6765+5765=12530
Als je dan alleen de gezinnen beschouwt met 4 kinderen van hetzelfde geslacht (dus: 12530 gezinnen), dan is de kans dat het alleen jongens zijn, gelijk aan⁶⁷⁶⁵/₁₂₅₃₀ $\approx$ 0,5399, ofwel 53,99%.

Ik kan goed begrijpen dat dit tegen je gevoel in gaat, ik kan me voorstellen dat je 51% zou verwachten. Toch is het wel te begrijpen dat dit niet klopt, het wordt gemakkelijker om dit te zien wanneer er een groter verschil is tussen de kans op een jongen of een meisje.

Stel dat de kans op een jongen 90% is, en de kans op een meisje 10%. Ga uit van 100 gezinnen. Als er 1 kind wordt geboren, dan verwacht je 0,9 $\times $ 100=90 'jongensgezinnen' (= gezinnen met alleen jongens als kind) en 0,1 $\times $ 100=10 meisjesgezinnen. Dit zie je in het linkerdeel van onderstaand boomdiagram.

Nu wordt een tweede kind geboren. In de jongensgezinnen (waarvan er al veel zijn) lukt het in 90% van de gevallen om een kind van hetzelfde geslacht te krijgen. Van het grote aantal jongensgezinnen blijft dus een groot deel jongensgezin, nu met twee kinderen (jongens). Na twee kinderen komt het aantal jongensgezinnen op 0,9 $\times $ 0,9 $\times $ 100=81 (zie het rechter deel van het boomdiagram).
Bij de meisjesgezinnen (waarvan er al veel minder waren) lukt het maar in een klein aantal gevallen (10%) om opnieuw een kind van hetzelfde geslacht te krijgen. Van het kleinere aantal meisjesgezinnen blijft naar verhouding een veel kleiner deel over: slechts 10%. Het aantal meisjesgezinnen komt op 0,1 $\times $ 0,1 $\times $ 100=1.
Na twee kinderen zijn in totaal nog 81+1=82 gezinnen met kinderen van hetzelfde geslacht, hiervan zijn 81 jongensgezinnen. De kans dat een gezin met twee kinderen van hetzelfde gelacht een jongensgezin is, komt hiermee op ⁸¹/₈₂ $\approx$ 0,988, ofwel 98,8%.
Na elk kind neemt het aantal meisjesgezinnen sterker af dan het aantal jongensgezinnen. De kans dat een gezin met kinderen van hetzelfde gelacht een jongensgezin is, wordt na elk kind dus steeds groter. Bij een kleiner verschil in kans, zoals bij jouw vraag, is dit effect minder groot, maar wel aanwezig.

Is het hiermee duidelijker geworden?
GHvD
25-6-2024

Dana en Zoya spelen een tennispartij

Dana en Zoya spelen een tennispartij over maximaal 5 sets. Degene die als eerste drie sets wint, is winnaar. De kans dat Dana een set wint is 0.55 dus voor Zoya is die kans 0.45

Bereken de kans dat de partij vier sets duurt.

Ik dacht zelf 3nCr1 x 0.45 tot de macht 3 x 0.55 + 3nCr1 x 0.55 tot de macht 3 keer 0.45 maar volgensmij hoeven die combinaties niet, waarom niet. Nouja, dat of ik heb het helemaal fout. Ik ontvang graag snel antwoord heb strakjes een toets.

Groet, sem
Sem
27-6-2024

Antwoord

Hallo Sem,

Een partij duurt 4 sets wanneer Dana 1 set wint en Zoya 3 sets, of andersom. Ofwel:

(1xD en 3xZ) of (1xZ en 3xD).

De kans op het spelverloop DZZZ is 0.55x0,45³. Echter, de D kan op 3 verschillende posities staan: ZDZZ en ZZDZ kunnen ook. (D mag niet als laatste, want dan is de partij al na 3 sets afgelopen). De kans op 1xD en 3xZ wordt hiermee:

3 x 0.55x0,45³

Op dezelfde wijze bereken je de kans dat Dana 3 sets wint. Deze kans wordt:

3 x 0.45x0,55³

Tel deze kansen op om de kans te vinden dat de partij 4 sets duurt, ongeacht wie de winnaar is.

Succes met je toets!
GHvD
27-6-2024