WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Goniometrie

Lengte en hoek van schuine raaklijn aan twee cirkels

Lengte en hoek van schuine raaklijn, tangent aan 2 niet rakende cirkels van verschillende diameter.
Wat is de formule om dit te berekenen?
bert a
11-3-2024

Antwoord

Hallo Bert,

Je vraag is niet helemaal goed doorgekomen, je hebt geprobeerd de gehele vraag in de titel in te vullen. Dat gaat niet goed ....

Ik vermoed dat je hoek S in onderstaande figuur wilt berekenen, de hoek tussen de raaklijn aan twee cirkels en de lijn door de middelpunten van de cirkels:

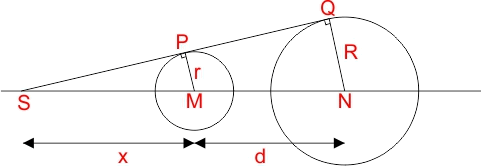
Dat kan als volgt:

De kleine cirkel heeft straal r, de grote cirkel heeft straal R. De afstand tussen de middelpunten M en N noem ik d. P en Q zijn de raakpunten van de raaklijn aan de cirkels.
De driehoeken SMP en SNQ zijn gelijkvormig. Dan geldt:

^x/_(x+d) = ^r/_R

Dus:

x·R = x·r+d·r
x(R-r) = d·r
x = ^d·r/_(R-r)

in driehoek SMP zie je:

sin(hoek S) = ^r/_x
sin(hoek S) = ^r/_{^d·r/_(R-r)}
sin(hoek S) = ^(R-r)/_d

dus:

Hoek S = arcsin(^(R-r)/_d)

Als je iets anders zocht, moet je dat maar even laten weten.
GHvD
12-3-2024

Vergelijking van een cirkel

Geef de vergelijking van de cirkel met middelpunt (3,2) en een punt P(6,6)
Zoe
18-3-2024

Antwoord

Gebruik de algemene vergelijking voor de cirkel. Bereken de afstand van middelpunt en $P$ en stel vervolgens de vergelijking op. Als het goed is kom je dan uit op:

$
\left( {x - 3} \right)^2 + \left( {y - 2} \right)^2 = 25
$

Hopelijk helpt dat.
4. cirkels, raaklijnen en afstanden

WvR
18-3-2024

Tangens

Wanneer moet je die -1 gebruiken bij het uitrekenen van Cosinus Sinus of Tangens? Of moet dat altijd bij een hoek berekenen
Fara E
21-3-2024

Antwoord

Op Wanneer gebruik je tangens en shift-tangens? staat wat je moet doen. Tan geeft de tangens bij een 'hoek' en tan^-1 geeft de 'hoek' bij een gegeven tangens.

Helpt dat?

Meer tips en truuks op Rekenen met sinus, cosinus en tangens
WvR
21-3-2024

Vereenvoudigen van goniometrische uitdrukkingen

Ik heb een vraag over de volgende oefeningen:
a) sin⁴x-cos⁴x/sin²x-cos²x
b) sin x - sin(x)cos²(x)

Ik begrijp niet hoe ik deze kan vereenvoudigen.

Alvast bedankt voor de hulp!
Y
19-4-2024

Antwoord

Gebruik daarbij dat
$
\sin ^2 x + \cos ^2 x = 1
$
$
a^2 - b^2 = (a + b)(a - b)
$
Je krijgt dan:

a.
$
\eqalign{
& \frac{{\sin ^4 x - \cos ^4 x}}
{{\sin ^2 x - \cos ^2 x}} = \cr
& \frac{{\left( {\sin ^2 x + \cos ^2 x} \right)\left( {\sin ^2 x - \cos ^2 x} \right)}}
{{\sin ^2 x - \cos ^2 x}} = \cr
& \sin ^2 x + \cos ^2 x = 1 \cr}
$

b.
$
\eqalign{
& \sin x - \sin x\cos ^2 x = \cr
& \sin x\left( {1 - \cos ^2 x} \right) = \cr
& \sin x \cdot \sin ^2 x = \cr
& \sin ^3 x \cr}
$

Zou dat lukken?
WvR
19-4-2024

Sinus en cosinus van een hoek bepalen

Ik snap niet hoe je de sinus en cosinus van een getal bepaald.

Laura
25-4-2024

Antwoord

Hallo Laura,

Voor deze vraag hoef je de sinus en cosinus van 15° niet daadwerkelijk uit te rekenen. Het is voldoende om in te zien dat voor hoeken tussen 0° en 90° geldt:
Bij een grotere hoek hoort een grotere sinus, en
Bij een grotere hoek hoort een kleinere cosinus
. Je kunt dit goed aflezen in de 'goniometrische eenheidscirkel'. Hoe je dit doet, zie je in het eerste deel van het filmpje Goniometrische getallen - Deel 1: Definitie van sinus, cosinus en tangens.

Om de sinus en cosinus te vinden van hoeken groter dan 90° gebruik je de eenheidscirkel om te beredeneren welke hoek uit het eerste kwadrant dezelfede sinus of cosinus heeft, eventueel met een min-teken. Hoe dit in zijn werk gaat, zie je in Goniometrische getallen - Deel 3: Sinus, cosinus en tangens van hoeken in kwadranten II, III, IV.

Probeer aan de hand van de uitleg in deze filmpjes de uitwerking van je opgave te volgen. Kom je er niet uit, laat dan maar weten waar je vastloopt.
GHvD
26-4-2024

Bewegingsvergelijkingen met goniometrische formules

Bij de vraag bereken in graden in één decimaal de hoek alfa die de baan in punt D ([¹/₂ $\sqrt{}$ 3 ; ¹/₂) maakt met de lijn y= ¹/₂

Ik weet dan niet wat je met de lijn moet doen y= ¹/₂

Ceylin
5-5-2024

Antwoord

De het punt $D$ ligt op de lijn $y=\frac12$ en de hoek tussen de baan en die lijn wordt gevraagd. De oplossing gebruikt de raakvector $\vec v$ aan de baan in $D$ en de richtingsvector $\vec r$ van de horizontale lijn. En de hoek wordt bepaalt via het inwendig product van die twee vectoren.

Zie het plaatje; omdat de lijn horizontaal is de tangens van $\alpha$ gelijk aan $\frac12\sqrt3$ (quotiënt van $y$- en $x$-coöordinaten van $\vec v$). Dat geeft hetzelfde antwoord.
kphart
5-5-2024

Re: Bewegingsvergelijkingen met goniometrische formules

Maar wat vul je precies in de richtingsvector?

Ceylin
5-5-2024

Antwoord

Niets.

De vector $\vec r$ is gewoon gegeven als de richtingsvector van de lijn $y=\frac12$. Van die lijn zijn, zo te zien, geen bewegingsvergelijkingen gegeven, en er hoort daarom ook geen tijdstip bij om het punt $D$ te bepalen.

Je zou bewegingsvergelijkingen kunnen geven: $x(t)=t$ en $y(t)=\frac12$, en dan geldt $x'(t)=1$ en $y'(t)=0$; dus welke $t$ je ook invult er komt altijd $\binom10$ als raakvector. Dan kun je net zo goed geen $t$ invullen.
kphart
6-5-2024

Re: Wat is een radiaal?

Het voorlaatste woord 'kilometers' moet natuurlijk kilometer\uur zijn; het is immers een snelheid.
Mart
12-5-2024

Antwoord

Het ging hier om afstandsgetallen, dus bijvoorbeeld zoiets als:

Ik denk dat het zo dus wel in order is. Het idee is duidelijk!
WvR
13-5-2024

Driehoek met omschreven cirkel

Gevraagd:

Beschouw een gelijkzijdige driehoek ABC met zijde 1. Laat M het middelpunt zijn van de cirkel omschreven rond deze driehoek. Laat punt D het beeld zijn van punt B na muntspiegeling rond M. Wat is de afstand van A tot D?

Wat ik heb geprobeerd:

Door de situatie te schetsen kreeg ik de indruk dat de driehoek ABD te verkrijgen is door punt C te schuiven langs de cirkel tot de positie van punt D, tevens is de afstand BD gelijk aan de diameter van de cirkel. Verder dan dit kom ik helaas niet...
Erik-J
26-5-2024

Antwoord

Hallo Erik-Jan,

Prima om een schets te maken:

Bekijk driehoek ABD met hoeken 90°, 30° en 60°. De zijden verhouden zich als 1:2:√3. Je weet: AB=1, dus met deze verhoudingen is zijde AD te berekenen.

Lukt het hiermee?
GHvD
26-5-2024

Re: Driehoek met omschreven cirkel

Veel dank voor het antwoord, het gaat mij alleen even iets te snel. Hoe weten we zo zeker dat de hoek BAD 90 graden en hoek ABD 30 graden is (ondanks dat het suggestief is door het plaatje)? Hoe komt u ook aan de verhouden 1:2: $\sqrt{3} $
Erik-J
26-5-2024

Antwoord

Hallo Erik-Jan,

Goed dat je doorvraagt wanneer (een deel van) een antwoord niet duidelijk is. Wij weten immers niet hoeveel achterliggende kennis je al hebt.

Allereerst hoek BAD. Je had zelf al gevonden dat BD een middellijn is van de cirkel. Voor elk punt A op de cirkel geldt dan dat hoek BAD een rechte hoek is, zie wikipedia: Stelling van Thales.

Dan hoek ABD. Trek vanuit M de hulplijnen MA, MB en MC, zie hieronder:

Zo ontstaan drie gelijke driehoeken AMB, BMC en CMA. Deze driehoeken zijn gelijkbenig, want de zijden MA, MB en MC zijn alle gelijk aan de straal van de cirkel. Hierdoor zijn de hoeken A₁, A₂, B₁, B₂, C₁ en C₂ allemaal gelijk. Elk van deze hoeken is zodoende ^180°/₆=30°. Dan blijft over voor hoek ADB: 180°-90°-30°=60°.

Driehoek BDA is een zgn. "30-60-90-graden driehoek", deze heeft vaste verhoudingen tussen de zijden. Dit kan je in de figuur hieronder zien. Driehoek PQR is zo'n 30-60-90-graden driehoek, deze is nog eens gespiegeld om PQ:

Op deze wijze ontstaat de gelijkzijdige driehoek SQR, met drie gelijke hoeken van 60°. De zijden van deze driehoek zijn 2, dus QR=2. P is het midden van RS, dus PR=1. Met Pythagoras is PQ dan te berekenen:

PQ = √(2²-1²) = √(4-1) = √3.

De driehoek met hoeken 30°, 60° en 90° komt veel voor, dus veel mensen nemen niet meer de moeite om bovenstaande afleiding steeds opnieuw te maken, maar leren uit het hoofd dat de zijden van zo'n "30-60-90-graden driehoek" zich verhouden als 1:2:√3. Hou hierbij goed in de gaten welke lengte bij welke zijde hoort: korte rechthoekszijde:schuine zijde:lange rechthoekszijde.

In onderstaande figuur geldt dus:

AD:AB = 1:√3
dus:
AD = ^AB/_√3 = ¹/_√3 = ¹/₃√3.

OK zo?
GHvD
26-5-2024

Re: Re: Driehoek met omschreven cirkel

Prachtig, veel dank! Nu snap ik ook het nut van de goniometrische functies meer (misschien was dit ook het achterliggende doel van de opgave, omdat het zonder moest). Met behulp van de tangens hadden we hem anders super snel uitgerekend, door simpelweg |AD| = tan 30 graden. Nogmaals bedankt, het is mij nu volstrekt duidelijk.
Erik-J
26-5-2024

Antwoord

Graag gedaan
GHvD
26-5-2024